Осмислення
способів доведення нерівностей.
На практиці
математики використовують для доведення різні способи:
- за визначенням(віднімання більшого
від меншого);
- способом додавання лівих та правих
частин класичних нерівностей;
- способом від супротивного;
- методом математичної індукції;
- штучні способи;
- синтез декількох способів доведення.
Означення
Для довільних дійсних чисел виконується нерівність
Доведення
перенесемо всі члени в ліву частину і помножино на 2:
виділимо повні квадрати:
Очевидно що рівність досягається тоді і тільки тоді, коли всі три числа рівні.
Завдання для самостійного опрацювання
Завдання для самостійного опрацювання
1.Довести
нерівність
x3(1+y)-1(1+z)-1 + y3(1+x)-1(1+z)-1 + z3(1+y)-1(1+x)-1 >=0,75,
якщо додатні усі дійсні змінні та xyz=1
2.Довести
нерівність
a2(a+2b3)-1+ b2(b+2c3)-1 + c2(a+2a3)-1>=1,
якщо
додатні усі дійсні змінні та a + b + c = 3.
3.Довести
нерівність
(1+a) (1+ b2)-1 +(1+b) (1+ c2)-1 +(1+c) (1+ a2)-1>=3,
якщо
додатні усі дійсні змінні та a + b + c = 3.
4.Довести
нерівність
(z+y+x)0,5 >=
(x-1)0,5 + (y-1)0,5 + (z-1)0,5
якщо
усі дійсні змінні не менше 1 та x -1 + y -1 + z-1 = 2.
5.Довести
нерівність
a3(a3+b3 +abc)-1+ b3(a3+c3 +abc)-1 + c3(a3+c3 +abc)-1>=1,
якщо
додатні усі дійсні змінні.
6.Довести
нерівність
(a2+1) (b2+1) (c2+1) >=8,
якщо
додатні усі дійсні змінні та ab+ cb + ac = 3.
Каталог класичних нерівностей:
1. Сума двох взаємно обернених додатних чисел не менше двох, тобто якщо для
чисел a∙b=1, тоді
a/b+b/a>=2
Сума двох взаємно обернених недодатних чисел не менше двох, тобто якщо для чисел a∙b= -1, тоді
a/b+b/a=<-2
2. Для невід’ємних n:
1/n+ n>=2
3.
Якщо
для невід’ємних чисел a∙b=1, тоді
(a+b)>=2.
4.
Якщо
для невід’ємних m чисел a∙b∙c∙d∙e∙…∙f=1, тоді
(a+b+c+d+e+…+f)> =m.
5. Для довільного
а вірно:
а2>=0.
6. Для довільної
послідовності чисел аі
вірно:
а12+ а22 +а32+ …+аn2>=0
7. Для додатного
числа а>0 та від’ємного
дискримінанта: b2-4aс<0 завжди виконується
квадратна нерівність:
ax2+bx+c>0.
8. Для від’ємного
числа а<0 та від’ємного
дискримінанта: b2-4aс<0 завжди виконується
квадратна нерівність:
ax2+bx+c<0.
Яку нерівність можна використати для доведення нерівності Несбіта:
Із нерівностей Коші-Буняковського і трьох квадратів отримуємо:

- з чого негайно слідує нерівність Несбіта.
- 1. Довести, що для будь-яких чиселa2+b2+c2>=ab+bc+ac.Вказівка. Додати окремо ліві та праві частини нерівностей:a2+b2 >= 2ab, с2+b2 >= 2сb, a2+с2 >= 2aс. Рівність досягається, якщо a=b=c.2.Довести, що для будь-яких чисел a, b, c, які мають однакові знаки:. a/b+b/c+ c/a>=33.Для додатних a, b дріб c+d/a+bлежить між дробами c/a та b/dДовести.4.Довести, що невід’ємних трьох дійсних чисел виконується нерівність:. ab/c+ac/b+ cb/a>=3
-
Визначення
Через граничний перехід довизначаються такі величини:
Часткові випадки

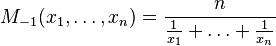 — середнє гармонійне (HM),
— середнє гармонійне (HM),![M_0(x_1,\dots,x_n) = \sqrt[n]{x_1\cdot\dots\cdot x_n}](http://upload.wikimedia.org/math/0/5/e/05e40c7677e45396178661635deb0605.png) — середнє геометричне (GM),
— середнє геометричне (GM), — середнє арифметичне (AM),
— середнє арифметичне (AM), — середнє квадратичне (RMS).
— середнє квадратичне (RMS).Нерівності[ред. • ред. код]
- Якщо
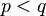 , тоді
, тоді  , і рівність наступає тільки при
, і рівність наступає тільки при 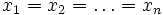 .
.
Це слідує з того, що  , що може бути доведено за допомогою нерівності Йєнсена.
, що може бути доведено за допомогою нерівності Йєнсена.
 , що може бути доведено за допомогою нерівності Йєнсена.
, що може бути доведено за допомогою нерівності Йєнсена.- Частковим випадком попередньої нерівності є:
Квазі-арифметичне середнє (середнє за Колмогоровим) для дійсних чисел  визначається як
визначається як
 визначається як
визначається якЧасткові випадки
- При
 — отримуємо середнє арифметичне,
— отримуємо середнє арифметичне, - При
 — отримуємо середнє геометричне,
— отримуємо середнє геометричне, - При
 — отримуємо середнє гармонійне,
— отримуємо середнє гармонійне, - При
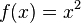 — отримуємо середнє квадратичне,
— отримуємо середнє квадратичне, - При
 — отримуємо середнє степеневе.
— отримуємо середнє степеневе.
У 1930 році А. М. Колмогоров довів, що будь-яка середня величина має вигляд функції  , якщо володіє властивостями:
, якщо володіє властивостями:
 , якщо володіє властивостями:
, якщо володіє властивостями:- неперервна та монотонна по кожному

- симетрична (значення не змінюється при перестановці аргументів)
- деяку групу значень можна замінити їх власним середнім, не міняючи спільного середнього.
Середні Колмогорова використовують в прикладній статистиці і економетриці.
Середнє зважене, точніше середнє арифметичне зважене для дійсних чисел  з ваговими коєфіцієнтами
з ваговими коєфіцієнтами 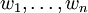 визначається як
визначається як
 з ваговими коєфіцієнтами
з ваговими коєфіцієнтами 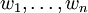 визначається як
визначається як
Коли всі вагові коефіцієнти рівні між собою 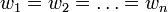 , середнє арифметичне зважене буде дорівнювати середньому арифметичному.
, середнє арифметичне зважене буде дорівнювати середньому арифметичному.
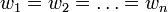 , середнє арифметичне зважене буде дорівнювати середньому арифметичному.
, середнє арифметичне зважене буде дорівнювати середньому арифметичному.
Існують також зважені версії середнього геометричного, середнього гармонійного, середнього степеневого, а також їх узагальнення —середнього за Колмогоровим.
Нерівність Чебишова для сум чисел
Нерівність Чебишова для сум чисел, названа на честь Пафнутія Львовича Чебишова, стверджує, що якщо
і
то
Аналогічно, якщо
і
то
Доведення[ред. • ред. код]
Нерівність Чебишова легко вводиться з нерівності перестановок:
Припустимо, що
і
Зважаючи на нерівність перестановок вираз
є максимально можливим значенням скалярного добутку даних послідовностей. Додаючи нерівності
одержуємо
або, розділивши на 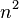 :
:
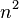 :
:Завдання для самостійного опрацювання
Нехай а, b, с – додатні дійсні числа. Доведіть, що
 .
.
 .
.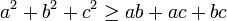
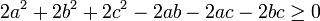







 —
— 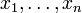 як:
як:
![M_0(x_1, \ldots, x_n) = \lim_{p\to 0} M_p(x_1, \ldots, x_n) = \sqrt[n]{x_1\cdot\dots\cdot x_n}](http://upload.wikimedia.org/math/e/a/2/ea27c29d98bebb5c3ee9310727773a0a.png)

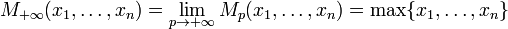


 —
— 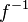 —
— 
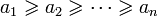
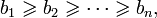


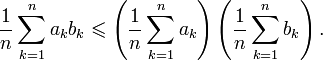



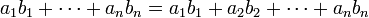



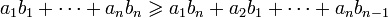





















Немає коментарів:
Дописати коментар