Розв′язати в натуральних числах рівняння:
2x +1= y2
Вказівка: Розглянемо
функції: f(n)= 2n +1 та f(n)= n2.
Графіки цих двох функцій перетинаються в двох точках, одна із яких має натуральні
значення координат точки, це точка (3; 9), а інша таких немає.
21+1=3;
22+1 =5;
23+1 =9=32 .
2p =(y +1)(y-1), а це можливо, якщо у=3,
отримаємо 23 =(3 +1)(3-1)=4*2.
2m +1m =(2 +1)(
2m-1 +2m-2 …+1)=3n.
Відповідь: х=3, у=3.
Розв′язати в натуральних числах рівняння:
a2+b2+c2 =59n .
Вказівка: 72+32+12 =59.
592 =(72+32+12)(72+32+12)=59*59=502 +302+92.
(50k2+9)2=2500k4+900k2+92=
(50k2)2 +(30k)2+ 92.
(7*59(n-1):2) 2+(3* 59(n-1):2 )2+(1*59(n-1):2)2 =59n.
Одна із трійок буде такою
a= 49*59(n-1):2
b= 9*59(n-1):2
c= 1*59(n-1):2,
де n- натуральне число.
Розв′язати в натуральних числах рівняння:
1.a2+b2+c2 =38n
2.a2+b2+c2 =74n
3.a2+b2+c2 =77n
Розв’язати
в цілих числах
х(х+1)
(х+7) (х+8) = у2.
Вказівка.
х(х+1)(х+7)(х+8) = х(х+8)(х+1)(х+7) =
=(х2+8х) (х2+8х+7)=
z(z+7), z = х2+8х
Якщо z>9
(z+3)2
=z2+6z+7< z2+7z< z2+6z+16<(z+4)2
Між
двома послідовними цілими квадратами не існує
квадрату цілого числа.
Тому
розглядаємо випадок х2+8х =z<=9.
Варто
розглянути такі рівняння:
х2+8х =-9;
х2+8х =-8;
х2+8х =-7;
х2+8х =-4;
х2+8х =-1;
х2+8х =0;
х2+8х =1;
Отримаємо розв’язки: (-9;-12), (-9; 12), (-8;0), (-7;0),
(-4; 12), (-4;-12), (-1;0), (0;0), (1; 12), (1;-12).
Розв’язати
в цілих числах
х6+3х3+1= у4.
Вказівка.
х>0
Оцінимо зверху та знизу:
(х3+1)2 = х6+2х3+1< х6+3х3+1=у4< х6+4х3+4<( х3+2)2
Між
двома послідовними цілими квадратами не існує квадрату цілого числа.
(х3+1)2 < у4 <( х3+2)2
х3+1< у2 < х3+2
Аналогічне
протиріччя отримуємо, для х>-1.
(х3+2)2 = х6+4х3+4< х6+3х3+1=у4< х6+2х3+1<( х3+1)2
-(х3+2)2 < у4 <-( х3+1)2
|х3+2|= -(х3+2)< у2 < -(х3+1)= |х3+1|
Це не виконується для цілих у.
Якщо х= -1, то у4 =-1. Немає розв’язку.
Якщо х= 0, то у4 = 1. Отже (0;-1), (0;1).
Розв’язати
рівняння в цілих числах x + y + z = xyz.
Вказівка. Від
кругової перестановки невідомих х на у, у на z, z на х рівняння
не змінює свого вигляду. Отже, якщо
розв’язок ( k,m,n), то розв’зком будуть і такі трійки чисел: ( n,k,m), ( m,n,k), ( n,m,k), ( k,n,m), ( m,k,n).
Якщо х2+у2+z2 =0. Отримаємо: х=у=z =0.
Якщо х2+у2+z2 <>0. Тоді 1/yz+ 1/xz + 1/yx =1.
Із рівності 1/2+ 1/3 + 1/6 =1. Отримаємо систему
рівнянь:
yz=2
xz=3
yx=6
Тому
розв’язок системи рівнянь: х = 3; у= 2; z =1.
Розглянемо випадки для цілих значень:
x + y + z = xyz.
1)Якщо хуz =0.
2)Якщо хуz =-1. х = 1; у= 1; z = -1.
3)Якщо хуz =1. х = 1; у= 1; z = 1.
4)Якщо хуz =2.
5)Якщо хуz =-2.
6)Якщо хуz =3.
7)Якщо хуz =-3.
8)Якщо хуz =4.
9)Якщо хуz =-4.
10)Якщо хуz =-5.
11)Якщо хуz =5.
12)Якщо хуz =6. х = 3; у=
2; z =1.
13)Якщо хуz =-6. х = -3; у= -2; z =-1.
Тотожними
перетвореннями отримаємо рівність :
z( xy-1)=x+y, у якої ліва і
права частини цілі.
Якщо х+у =0, z=0 або xy-1 =0, тому
якщо xy-1 =0, у цілих числах отримаємо дві рівність
xy=1 , x=-y виконується,
якщо x=-1, y=-1 або x= 1, y= 1.
якщо z =0, у цілих числах рівність xy=1 виконується,
якщо x=-1, y=-1 або x= 1, y= 1.
Якщо х+у =n, z=n або xy-1 =1, тому у цілих
числах рівність xy=2 виконується, якщо x=2, y=1 або x= -2, y= 1.
Якщо х+у =0, z=0 або xy-1 =0, тому у
цілих числах рівність xy=1виконується, якщо x=-1, y=-1 або x= 1, y= 1.
Відповідь.
( -m,m,0), ( -m,0,m), ( 0,m,-m), ( 0,-m,m), ( m,0,-m) ( m,-m,0), де m - ціле число.
( 1,2,3), ( 1,3,2), ( 2,3,
1), ( 2,
1,3), ( 3,1,2
) (3,2,1).
Діофантові рівняння — невизначені поліноміальні рівняння з цілими коефіцієнтами, в яких невідомі змінні можуть набувати тільки цілих значень. Названі на честь давньогрецького математика Діофанта александрійського.
Діофантовим рівнянням 1-го ступеня (лінійним) з  невідомими називається рівняння вигляду
невідомими називається рівняння вигляду 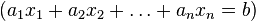 , де всі коефіцієнти і невідомі — цілі числа і хоча б одне
, де всі коефіцієнти і невідомі — цілі числа і хоча б одне 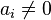
 невідомими називається рівняння вигляду
невідомими називається рівняння вигляду 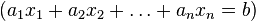 , де всі коефіцієнти і невідомі — цілі числа і хоча б одне
, де всі коефіцієнти і невідомі — цілі числа і хоча б одне 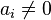
Розв'язком діофантового рівняння буде n цілих чисел 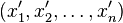 , що задовольняє
, що задовольняє 
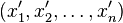 , що задовольняє
, що задовольняє 
Теорема 1 Лінійне діофантове рівняння з двома невідомими  можна розв'язати в цілих числах тоді й тільки тоді, коли число
можна розв'язати в цілих числах тоді й тільки тоді, коли число  ділиться націло на НСД(а, b)
ділиться націло на НСД(а, b)
 можна розв'язати в цілих числах тоді й тільки тоді, коли число
можна розв'язати в цілих числах тоді й тільки тоді, коли число  ділиться націло на НСД(а, b)
ділиться націло на НСД(а, b)
Теорема 2 Лінійне діофантове рівняння з двома невідомими  можна розв'язати в цілих числах тоді і тільки тоді, колиНСД(а, b) =1, НСД(а, b, с)=1, тобто, цілі числа а та b — взаємно прості, (не мають спільного дільника, крім 1).
можна розв'язати в цілих числах тоді і тільки тоді, колиНСД(а, b) =1, НСД(а, b, с)=1, тобто, цілі числа а та b — взаємно прості, (не мають спільного дільника, крім 1).
 можна розв'язати в цілих числах тоді і тільки тоді, колиНСД(а, b) =1, НСД(а, b, с)=1, тобто, цілі числа а та b — взаємно прості, (не мають спільного дільника, крім 1).
можна розв'язати в цілих числах тоді і тільки тоді, колиНСД(а, b) =1, НСД(а, b, с)=1, тобто, цілі числа а та b — взаємно прості, (не мають спільного дільника, крім 1).Історія
- Рівняння вигляду P(x, y,…,z)=0, де P(x, y,…,z)=0 многочлен декількох змінних із цілими коефіцієнтами, для яких потрібно знайти цілі розв'язки, називають діофантовими рівняннями. Названі вони ім'ям грецького математика Діофанта, який жив у ІІІ столітті н. е. Його книга «Арифметика» містила 189 задач із цілими числами, для кожної з яких наводилося один або декілька розв'язків.
Розв'язати діофантове рівняння означає:
- a) з'ясувати, чи має рівняння хоча б один ненульовий розв'язок у цілих числах;
- b) якщо рівняння має розв'язок в цілих числах, то з'ясувати скінченна чи нескінченна множина його розв'язків;
- c) знайти всі цілі розв'язки рівняння.
Лінійні діофантові рівняння виду навчились розв'язувати ще до Діофанта. Стародавні греки знали, що якщо це рівняння має розв'язок 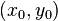 , то йому буде задовольняти нескінченна множина пар (x, y) виду
, то йому буде задовольняти нескінченна множина пар (x, y) виду 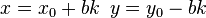 , де k — будь яке ціле число.
, де k — будь яке ціле число.
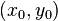 , то йому буде задовольняти нескінченна множина пар (x, y) виду
, то йому буде задовольняти нескінченна множина пар (x, y) виду 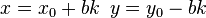 , де k — будь яке ціле число.
, де k — будь яке ціле число.Математики Стародавньої Греції та Стародавньої Індії знали методи розв'язання деяких рівнянь другого степеня вигляду ax²+bxy+cy²=dz² . Зокрема їм були відомі всі піфагорові трійки натуральних чисел x, y, z, що задовольняють рівнянню x²+y²=z² . Всі трійки взаємно простих піфагорових чисел стародавні математики знаходили за формулами x=m²-n², y=2mn, z=m²+n² , m, n — натуральні числа, n>m.
У 20-х роках ХХ сторіччя англійський математик Морделл висунув гіпотезу, що рівняння вищого степеня, ніж третій, можуть мати лише скінчену кількість цілих розв'язків. Цю гіпотезу було доведено голландським математиком Фалтінгсом 1983 року[Джерело?].
Особливе місце серед діофантових рівнянь посідає рівняння  , де n — натуральне число. Французький математик П'єр Ферма стверджував, що для n>2 це рівняння не має розв'язків у натуральних числах. Однак довести це твердження, яке назвалиВеликою теоремою Ферма, виявилося не так просто.
, де n — натуральне число. Французький математик П'єр Ферма стверджував, що для n>2 це рівняння не має розв'язків у натуральних числах. Однак довести це твердження, яке назвалиВеликою теоремою Ферма, виявилося не так просто.
 , де n — натуральне число. Французький математик П'єр Ферма стверджував, що для n>2 це рівняння не має розв'язків у натуральних числах. Однак довести це твердження, яке назвалиВеликою теоремою Ферма, виявилося не так просто.
, де n — натуральне число. Французький математик П'єр Ферма стверджував, що для n>2 це рівняння не має розв'язків у натуральних числах. Однак довести це твердження, яке назвалиВеликою теоремою Ферма, виявилося не так просто.Діофантові рівняння першого степеня
Рівняння виду ax+by=c, де a, b, c — числа, а x, y- змінні, називають діофантовим рівнянням першого степеня з двома змінними. Для розв'язання рівняння застосовують наступні теореми.
- Теорема1. Якщо a i b — взаємно прості числа, то для будь якого цілого c, рівняння має хоча б один розв'язок у цілих числах.
- Теорема2. Якщо a i b мають спільний натуральний дільник d<>1 , а ціле число c не ділиться на d, то рівняння ax+by=c не має розв'язків в цілих числах.
- Теорема3. Якщо a i b — взаємно прості числа, то рівняння ax+by=c має нескінченну кількість розв'язків, які знаходять за формулами
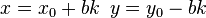 , де
, де 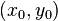 — будь-який цілий розв'язок цього рівняння, k є Z.
— будь-який цілий розв'язок цього рівняння, k є Z.
Частинний розв'язок 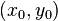 для малих a i b можна знайти підбором, а у випадку, коли числа a i b великі, скористувавшись наступною теоремою:
для малих a i b можна знайти підбором, а у випадку, коли числа a i b великі, скористувавшись наступною теоремою:
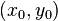 для малих a i b можна знайти підбором, а у випадку, коли числа a i b великі, скористувавшись наступною теоремою:
для малих a i b можна знайти підбором, а у випадку, коли числа a i b великі, скористувавшись наступною теоремою:- Теорема4. НСД(a, b)=d може бути записаний у вигляді d=am+bn, де m, n — цілі числа.
Приклади
- Лінійне рівняння:
Це рівняння має розв'язок тоді й лише тоді коли найбільший спільний дільник  ділить a.
ділить a.
 ділить a.
ділить a.
Має розв'язок тоді і тільки тоді коли d = НСД(a, b).
 :
:- При
 розв'язками рівняння будуть піфагорові трійки
розв'язками рівняння будуть піфагорові трійки - Велика теорема Ферма стверджує, що рівняння не має розв'язків для
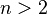 .
.
- При
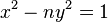 , де n не є точним квадратом — рівняння Пелля
, де n не є точним квадратом — рівняння Пелля , де
, де 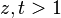 , — рівняння Каталана
, — рівняння Каталана для
для 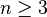 і
і  — рівняння Туе
— рівняння Туе
Нерозв'язність у загальному вигляді[ред. • ред. код]
Десята проблема Гільберта, сформульована 1900 року, полягає пошуку алгоритму для розв'зання довільних алгебраїчних діофантових рівнянь. 1970 року Юрій Матіясевіч довів алгоритмічну нерозв'язність цієї проблеми[1].
Історична довідка про діофантові рівняння.
Давньогрецький математик Діофант
представляє одну із найцікавіших особистостей в історії математики. Ми не
знаємо, ким був Діофант, точні роки його життя, не відомі його попередники, які
працювали у тій же сфері, що й він.
Дуже
цікавою є діяльність Діофанта. До нас дійшло 7 книг із 13, які були об’єднані в
«Арифметику». Стиль і зміст цих книг дуже відрізняється від класичних книг з
теорії чисел та алгебри, зразки яких ми знаємо з «Начал» Евкліда, лем Архімеда
і Аполлонія. «Арифметика», безсумнівно, є результатом багаточисленних
досліджень, велика кількість з яких залишилась нам невідомою.
«Арифметика»
Діофанта – це збірник задач (їх всього 189), кожна з яких має розв'язок і
необхідні пояснення. В збірник входять різноманітні задачі, і їх розв’язки дуже
часто не так просто зрозуміти.
Діофант практикувався у знаходженні розв’язків невизначених рівнянь вигляду квадратного та кубічного , або систем
таких рівнянь. Його цікавили тільки додатні цілі числа і раціональні розв’язки.
Ірраціональні розв’язки він називав «неможливими» і ретельно підбирав
коефіцієнти так, щоб отримати шукані додатні, раціональні розв’язки.
Тому
,зазвичай, довільне невизначене рівняння (але, як правило, з цілими
коефіцієнтами)називають «діофантовим», якщо хочуть наголосити на тому, що
рівняння слід розв’язувати в цілих числах.
Невизначені
рівняння першого степеня почали розглядати математики, приблизно в V столітті.
Деякі такі рівняння з двома, трьома невідомими з’явились у зв’язку з
проблемами, які виникли в астрономії, наприклад, при розгляді питань, пов’язаних
з визначенням періодичного повторення небесних явищ.
В
1624 році була опублікована книга французького математика Баше де
Мезирьяка , у якій для розв'язку рівняння 𝑎𝑥+𝑏𝑦=𝑐 фактично застосовується процес, що
зводиться до послідовного визначення неповних часткових підхідних дробів.
Після
Баше в XVII і XVIII століттях різні алгоритми для розв'язку невизначеного
рівняння першого степеня з двома невідомими давали Роль, Ейлер та інші
математики.
Ланцюгові
дроби для розв'язку таких рівнянь були застосовані вперше Лагранжем. Пізніше
діофантові рівняння стали записувати і розв’язувати у формі конгруенцій.
У
серпні 1900 року в Парижі відбувся ІІ міжнародний конгрес математиків. 8 серпня
Д. Гільберт прочитав на цьому конгресі доповідь «Математичні проблеми». Серед
23 проблем, розв'язок яких, як вважав Гільберт, було необхідно отримати в наступному
XX столітті , десяту проблему він сформулював наступним чином:
«Нехай
задано діофантове рівняння з довільним числом невідомих і раціональними
числовими коефіцієнтами. Вказати спосіб, за допомогою якого можна після
скінченного числа операцій встановити, чи розв’язне це рівняння в цілих числах
».
Гіпотезу,
що такого способу не існує, першим сформулював (з вагомими на те доказами)
американський математик М. Девіс у 1949 році. Доведення цієї гіпотези
затягнулося на 20 років – останній крок був зроблений в 1970 році Юрієм
Володимировичем Мятиясеєвичем , на першому році аспірантури він показав
алгоритмічну нерозв’язність 10 –ї проблеми Гільберта.
Проте,
якщо про довільне діофантове рівняння не можна сказати чи має воно цілі корені,
чи не має, то проблема існування цілих коренів лінійного діофантового рівняння
розв’язана.
Курсова
робота складається з двох розділів. У першому розділі розглядаються лінійні
діофантові рівняння, основні теореми, що дають можливість знаходити розв’язки
цих рівнянь або визначати їх кількість, а також деякі невизначені рівняння
вищих порядків , що розв’язуються в цілих додатних числах за відомими
алгоритмами.
Діофантові рівняння - вам це варто прочитати.
Приклади для самостійного опрацювання.
Діофантове рівняння x3+y3+z3= u3 має безліч
розв′язків типу
63+13+83=93 33+43+53=63
(6k; k; 8k; 9k) (3k; 4k; 5k; 6k), де k ціле число
а загальні розв′язки мають вигляд для цілих чисел r та s:
x=28r2+11rs-3s2
y=21r2-11rs-4s2
z=35r2+7rs+6s2
u=-42r2-7rs-5s2
Розв′язати
рівняння в цілих числах.
1.хk + уk = zk+1
Вказівка.
Поділити все рівняння на zk. І обгрунтувати, що х=z та z=y.
Відовідь:
(2; 2; 2), якщо k-
додатне ціле число.
2.х-k + у-k = z1-к
Вказівка.
Поділити все рівняння на zk. І обгрунтувати, що х=z=y=2.
3.xy +z = уx
Вказівка.
Поділити все рівняння на yx. І обґрунтувати монотонність
лівої частини рівняння, тому х=m та y=m, тобто (m; m;0), де m - ненульове додатне ціле число.
4.
(х - у)2 = х + у
Вказівка.
Запропонувати
заміну у рівнянні на х – у = n. І обгрунтувати, що х + y = n2. Розв′язати
систему двох лінійних рівнянь відносно невідомих.
5.(ху - 7)2 = х2
+ у2
Вказівка.
Запропонувати
заміну у рівнянні на ху – 7 = n. І обгрунтувати, що х + y = (n -7)2. Розв′язати
систему двох лінійних рівнянь відносно невідомих.
Відовідь:
(3; 4), (4; 3), (7; 0), (0; 7).
6. х2 = x
- y
Вказівка.
Запропонувати
заміну у рівнянні на х-у = n. І отримати, що х2 = n. Розв′язати систему двох лінійних рівнянь відносно невідомих.
7. х2у3= х4у5
Вказівка.
(0;0),(-1;-1). (1;1),( 1;-1),(-1; 1)
Запропонувати поділити
рівняння на х2у3. І отримати, що х2у2= 1. Розв′язати рівняння ху= 1 ху= -1 двох лінійних рівнянь відносно невідомих.
8. х2 + у2 = х3 + у3
Вказівка. у3 -
у2 = х3 - х2 ; у2(у – 1)= х2(х – 1);
у2(у
– 1)/х2(х
– 1) =1; тому розглянути випадки:
a) у2(у – 1)=0; b)у2(у – 1)=1; c)y=m;
9. х2у2= х7у7
Вказівка. х5у5 =1; ху=1. Отже пара цілих чисел: (m; m), де m – ціле число.
10. х2 + у2 + z2= хy + уz + zx
Вказівка. Помножити рівняння на два і виділити повні
квадрати. Тоді (х-у)2 + (у-z)2 + (x-z)2 =0; звідки z =n. Отже трійка чисел: (k; k; k), де k – ціле число.
11.хy + уz + zx=1
Вказівка. Якщо х = k; y = 1-k; Тоді k(1-k) + (1-k)z + zk =1; звідки z =1-k+k2.
Отже трійка чисел: (k; 1-k; 1-k+k2), де k – ціле число.
12.х3
+ у3 + z3=0
Отже
трійка чисел: (k; -k; 0), (-k; k; 0), (0; -k; k), (0; k; -k), (-k; 0; k), (k; 0; -k), де k – ціле число.
13.хy + уz + zx=0
Вказівка.
Повним перебором усіляких трійок (k; m; n), де цілі значення : -1,
0 та +1, отримаємо: (0; 1; -1), (-1; 0; 1).
14.хy + уz + zx=1
Вказівка. (1; 1;
-1), (-1; 1; 1), (1; -1; 1).
15.хy + уz + zx=2
Вказівка. (-1; 0; 1), (1; -1; 0), (0; 1; -1),
16.хy + уz + zx=3
Вказівка. (1; 1; 1), (1; 0; 2), (2; 1; 0), (0; 2; 1).
17.
х2 + у2 + z2= х3 + у3 + z3
18.
х2у2z2= х3у3z3
19.
х3 +2у3 = 4z3
20. х3 - у5 = 4(x+y)2
21. х5 – у2 = 4
22. х2(y-1) – у2(x-1) = 1
23. (-х2 +у2 – 4)(x+1) = х2
Вказівка.
Так як числа х2 та x+1 взаємно прості, то треба
розглядати випадки: а)х2=x+1; б) -х2=x+1; в) x+1=1; г) x+1=-1
та підставити ці значення у дане
рівняння.
24. (y2+х) (x2+у) = (х-у)3
Вказівка.
Так як число x-у = n - ціле, то треба
розглядати випадки: а) x-у = 0; б) x-у = 1; в) x-у =-1; г) x-у = n та
підставити ці значення у дане рівняння.
Відповідь:
(0;0), (-1;-1), (n;0).
25.
х2 +у3 +z5= t7
Вказівка.
НСК(2;3;5;7)=210. Однак:128=27. 102 +33 +15= 27 . Оскільки, 210:2=105, тому х=10n105k;
Оскільки, 210:3=70, тому у=3n70k;
Оскільки,
210:5=42, тому z=1n42k;
Оскільки,
210:7=30, тому t=2n30k;
Відповідь:
(0; 0; 0; 0), (10n105k; 3n70k; n42k; 2n30k)
(-10n105k; 3n70k; n42k; 2n30k), n, k –цілі числа.
Цілочисельна
функція F(n, k) = [|n|/n] k
Значення
функції F(n, k)
F(n, k) = [|n|/n] k=1,
якщо n – ненульове ціле число, k- парне ціле число або якщо m – додатне ціле число, р- ціле число.
F(n, k) = [|n|/n] k=-1, якщо n – від′ємне
ціле число, k- непарне число.
Розв′язати
рівняння в цілих числах.
[|n|/n] k = 1
Відовідь:
(m; p), де m –
додатне ціле число, р- ціле число.
(s; t), де s – від′ємне ціле число, р- парне ціле
число.
[|n|/n] k =
-1
Відовідь:
(m;
p), де m
– від′ємне ціле число, р- ціле число.
[-|n|/n] k =
1
Відовідь:
(m;
2p), де m–
ненульове ціле число, р- ціле число.
[-|n|/n] k = -1
Відовідь:
(m; 2p-1), де m
– додатне ціле число, р- ціле число.
[-|n|/n] k =
[-|k|/k] n
Відовідь:
(m;
m), де m
– ненульове ціле число,
[-|n|/n] k = [|k|/k] n
Відовідь:
(m;
2m), де m
– ненульове додатне ціле число,
(2m; m),
де m – ненульове від′ємне ціле
число.
АЛГЕБРАЇЧНІ
ЗАДАЧІ ОЛІМПІАД З МАТЕМАТИКИ
1. Чи вірно,
що рівняння
А) (n - 7)(n + 1)(n + 7)(n - 1) + 455 = 0;
Б) (k - 2)(k + 1)k(k - 1) - 24 = 0;
В) (m - 7)(m + 1)(m + 7)(m - 1) + 432 = 0;
Г) (a - 3)(a + 1)(a + 3)(a - 1) - 105 = 0
мають єдиний розв’язок в натуральних
числах?
2. Які цілі вирази
А) (n - 7)(n + 1)(n + 7)(n - 1) + 576;
Б) (m- 2)(m + 1)m(m - 1) + 1;
В) (k - 3)(k + 1)(k + 3)(k - 1) + 16;
Г) (p - 4)(p + 2)(p + 4)(p - 2) + 36;
Д) (t - 5)(t + 3)(t + 5)(t - 3) + 64;
Е) (x - 1)(x + 3)(x + 2)(x -
2)(x
+ 1)(x
- 3) + 36;
Є) (y - 5)(y + 1)(y + 5)(y - 1) + 144
являються точними квадратами цілих
виразів з цілими коефіцієнтами?
3. Невід’ємні цілі числа x, y, z задовольняють рівність
30х + 32у + 33z = 447. Знайдіть значення виразу х + у + z.
Приклад.
Розв’язок діофантового рівняння
2x - 3y
+ 7z
= 1.
знайдемо у вигляді трійки
чисел, яка задана через один цілий параметр k:
х
= m1k + n1,
y = m2k + n2,
z = m3k + n3.
Для рівняння
am1 + bm2 + cm3
= d
знайдемо у вигляді трійки
чисел, яка задана через один цілий параметр k:
х
= m1k + n1,
y = m2k + n2,
z = m3k + n3.
Методом
невизначених коефіцієнтів отримаємо формули:
am1 + bm2 + cm3
= 0
аn1 + bn2 + сn3= d .
Для даного конкретного рівняння маємо рівності:
2m1 - 3m2 + 7m3
= 0
2n1 - 3n2 + 7n3= 1
Методом підбору(а це дає змогу
моделювати за певними умовами необхідні нам властивості невідомих трійок, а
якщо вам важко підбирати числа для розв’язку, то задавайте, двом будь-яким
невідомим довільні цілі числа і знаходьте третє невідоме із самого рівняння) знаходимо по одній цілій трійки чисел:
(m1 , m2 , m3) = (2, 6,
2)
(n1 , n2 , n3) = (1, -2,
-1)
Таким чином,
маємо трійку-розв’язок (x,
y,
z)т з одним цілим
параметром.
х
= 2k + 1,
y = 6k -2,
z = 2k - 1.
Перевірка.
2(2k
+ 1) – 3(6k -2)+
7(2k
-
1) = 1,
4k
+ 2
– 18k + 6
+ 14k -
7 = 1,
0*k
+1
= 1,
1=1.
Остаточно, нами
створено один із розв’язків такого прозорого матричного рівняння:
(2 -3 7)(
|
n1
|
m1
|
0
|
)(
|
1
|
)=
|
1
|
||
n2
|
m2
|
0
|
k
|
(8)
|
|||||
n3
|
m3
|
0
|
0
|
Тобто
виконується така рівність:
(2 -3 7)(
|
2
|
1
|
0
|
)(
|
1
|
)=
|
1
|
||
6
|
-2
|
0
|
k
|
||||||
2
|
-1
|
0
|
0
|
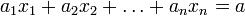

xy=x+y
ВідповістиВидалити