Нерівність Ердеша-Морделла — наступна нерівність:
Якщо  точка всередині трикутника
точка всередині трикутника  , а
, а  основи перпендикулярів опущених з точки
основи перпендикулярів опущених з точки  на сторони
на сторони  відповідно, то
відповідно, то
 точка всередині трикутника
точка всередині трикутника  , а
, а  основи перпендикулярів опущених з точки
основи перпендикулярів опущених з точки  на сторони
на сторони  відповідно, то
відповідно, тоПро нерівність
Нерівність вперше була сформульована Палом Ердешем у журналі American Mathematical Monthly у 1935 році і у цьому ж році була доведена Морделлом. Найвідоміші доведення - це доведення Андже Авеза через теорему птолемея, Леона Банко через подібністьтрикутників і обрахунок кутів, Вілмоса Коморніка через площі, а також Луіса Морделла із використанням тригонометрії.
Доведення
Для початку доведемо нерівність  (єдина різниця між доведеннями перечисленими вище є, як вони доводять цю нерівність). Наведемо класичне доведення цієї нерівності.
(єдина різниця між доведеннями перечисленими вище є, як вони доводять цю нерівність). Наведемо класичне доведення цієї нерівності.
 (єдина різниця між доведеннями перечисленими вище є, як вони доводять цю нерівність). Наведемо класичне доведення цієї нерівності.
(єдина різниця між доведеннями перечисленими вище є, як вони доводять цю нерівність). Наведемо класичне доведення цієї нерівності.
Застосувавши теорему синусів, до нерівності  отримаємо,
отримаємо,
 отримаємо,
отримаємо,
остання нерівність негайно слідує, з того, що величина проекції відрізку 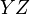 на пряму
на пряму 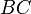 не перевищуватиме величину самого відрізка.
не перевищуватиме величину самого відрізка.
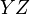 на пряму
на пряму 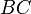 не перевищуватиме величину самого відрізка.
не перевищуватиме величину самого відрізка.
Аналогічно можна довести, що  та
та  , додавши три нерівності і застосувавши між нерівність Коші, для двох елементів отримаємо
, додавши три нерівності і застосувавши між нерівність Коші, для двох елементів отримаємо
 та
та  , додавши три нерівності і застосувавши між нерівність Коші, для двох елементів отримаємо
, додавши три нерівності і застосувавши між нерівність Коші, для двох елементів отримаємоСхожі нерівності
Часто на математичних олімпіадах пропонують нерівності, які схожі на нерівність Ердеша Морделла тобто теж пов'язують величини 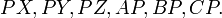
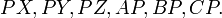
Зокрема нерівність, що була доведена Луісом Морделлом у 1962:
Такі нерівності часто доводять використовуючи, що
 і
і 
Класичні нерівності в трикутнику
Перша нерівність була доведена нами раніше, доведемо другу.
Нехай 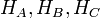 основи перпендикулярів опущених, з вершин
основи перпендикулярів опущених, з вершин  на сторони
на сторони  .
. 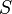 — площа трикутника.
— площа трикутника.
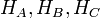 основи перпендикулярів опущених, з вершин
основи перпендикулярів опущених, з вершин  на сторони
на сторони  .
. 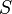 — площа трикутника.
— площа трикутника.
Зауважимо, що 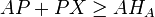 і
і  виразивши з останього
виразивши з останього  і поклавши його в перше отримаємо
і поклавши його в перше отримаємо
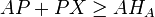 і
і  виразивши з останього
виразивши з останього  і поклавши його в перше отримаємо
і поклавши його в перше отримаємо
Чевіа́на — будь-який відрізок, що сполучає вершину трикутника та одну з точок на протилежній їй стороні. Частковими випадками ємедіана, симедіана, бісектриса та висота. Назва походить від імені італійського інженера Джованні Чеви, який 1678 року сформулював і довів відому теорему Чеви, що також названа його іменем.
Довжина
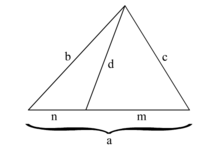
Довжина чевіани визначається з теореми Стюарта. Довжина відрізка  з малюнку визначається як:
з малюнку визначається як:
 з малюнку визначається як:
з малюнку визначається як:
Якщо чевіана є медіаною, маємо
або
оскільки
Якщо чевіана є бісектрисою, то формула перетворюється на
Якщо чевіана є висотою:
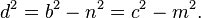
- Теорема Чеви — відома теорема класичної геометрії. Нехай дано трикутник ABC, і точки D, E, і F, що лежать на прямих BC, CA, і AB відповідно. Теорема стверджує, що лінії AD, BE і CF конкурентнітоді і тільки тоді якщо:
 Є також аналогічне тригонометричне формулювання Теореми Чеви, а саме AD, BE, CFконкурентні тоді і тільки тоді:Теорему довів в 1678 році Джованні Чева в праці De lineis rectis, але її також довів набагато раніше Юсуф Аль-Мутаман ібн Худ, король Сарагоси в XI столітті.
Є також аналогічне тригонометричне формулювання Теореми Чеви, а саме AD, BE, CFконкурентні тоді і тільки тоді:Теорему довів в 1678 році Джованні Чева в праці De lineis rectis, але її також довів набагато раніше Юсуф Аль-Мутаман ібн Худ, король Сарагоси в XI столітті.
- Медіана поділяє трикутник на два трикутники з рівними площами, а три проведені медіани — на шість рівновеликих.
- Медіани трикутника перетинаються в точці, яка є його центром мас.
- Медіана прямокутного трикутника, проведена до гіпотенузи, ділить трикутник на два рівнобедрені трикутники, та дорівнює половині гіпотенузи.
- В точці перетину медіани трикутника діляться в відношенні 2:1.
- При перетворенні медіана переходить в медіану.
- Якщо дві медіани трикутника перпендикулярні, то сума квадратів сторін, на які вони опущені, у п'ять разів більша за квадрат третьої сторони.
Математичні залежності
Довжина медіани визначається з рівняння:
визначається з рівняння: ,
,
де — сторона трикутника, на середину якої опущена медіана;
— сторона трикутника, на середину якої опущена медіана; 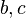 — інші сторони трикутника.Сума квадратів медіан довільного трикутника становить 3/4 від суми квадратів його сторін:
— інші сторони трикутника.Сума квадратів медіан довільного трикутника становить 3/4 від суми квадратів його сторін: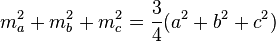 .
.
Довжина сторони трикутника через медіани визначається наступним чином: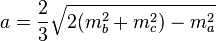 ,
,
де медіани до відповідних сторін трикутника,
медіани до відповідних сторін трикутника,  — сторони трикутника.
— сторони трикутника.- Бісектри́са (лат. bis — двічі і лат. secare — розсікати, розтинати) — термін, що вживається вгеометрії для позначення кількох споріднених понять[1]:
- Бісектриса кута — промінь, що проходить через вершину кута і ділить його навпіл. Кожна точка бісектриси однаково віддалена від сторін кута.
- Бісектриса трикутника — відрізок бісектриси одного з кутів цього трикутника від вершини кута до перетину з протилежною стороною.
Властивості
- Теорема про бісектрису: Бісектриса внутрішнього кута трикутника ділить протилежну сторону у відношенні, рівному відношенню двох прилеглих сторін
- Бісектриси внутрішніх кутів трикутника перетинаються в одній точці — інцентрі — центрі вписаного в цей трикутник кола.
- Бісектриси одного внутрішнього та двох зовнішніх кутів трикутника перетинаються в одній точці. Ця точка — центр одного з трьох зовнівписаних кіл цього трикутника.
- Основи бісектрис двох внутрішніх та одного зовнішнього кутів трикутника лежать на одній прямій, якщо бісектриса зовнішнього кута не є паралельною протилежній стороні трикутника.
- Якщо бісектриси зовнішніх кутів трикутника не паралельні протилежним сторонам, то їх основи лежать на одній прямій.
- Якщо в трикутнику дві бісектриси рівні, то трикутник — рівнобедрений (теорема Штейнера — Лемуса).
- Побудова трикутника за трьома заданим бісектрисами за допомогою циркуля та лінійки неможлива,[2] причому навіть за наявностітрисектора.[3]
- В рівносторонньому трикутнику бісектриса кута, протилежного до основи трикутника, є медіаною та висотою.
- Відстані від сторін кута до будь-якої точки бісектриси однакові.
- Кожна бісектриса трикутника ділиться точкою перетину бісектрис у відношенні суми довжин прилеглих сторін до довжини протилежної, рахуючи від вершини.
Формули за участю довжини бісектриси
Де: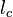 — бісектриса, проведена до сторони с
— бісектриса, проведена до сторони с — сторони трикутника проти вершин A, B,C відповідно
— сторони трикутника проти вершин A, B,C відповідно — довжини відрізків, на які бісектриса
— довжини відрізків, на які бісектриса 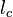 ділить сторону с
ділить сторону с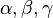 — внутрішні кути трикутника, що лежать навпроти сторін а, b,c відповідно
— внутрішні кути трикутника, що лежать навпроти сторін а, b,c відповідно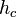 — висота трикутника, опущена на сторону c.
— висота трикутника, опущена на сторону c.
Теорема про бісектрису встановлює зв’язок між довжиною сторони протилежної до одного з кутів трикутника та довжинами двох інших сторін.Нехай дано трикутник ABC, а бісектриса кута A перетинає сторону BC в точці D. Теорема про бісектрису стверджує, що відношення довжин відрізків BD та DC дорівнює відношенню довжин сторін AB та AC.В загальному випадку, якщо пряма AD ділить кут A довільним чином тоді: - Бісектриса трикутника. Виконується співвідношення BD: DC = AB: AC

- Висота́ трику́тника — відрізок, проведений з вершини кута до протилежної сторони або до продовження протилежної сторони і лежить на прямій, перпендикулярній до цієї сторони. Ця сторона називається основою трикутника. Точка перетину сторони і перпендикуляра називається основою перпендикуляра. Довжина висоти — це відстань від вершини до основи трикутника.Висоту використовують для обчислення площі трикутника: половина добутку довжини висоти на довжину основи дорівнює площі трикутника.
- де h — висота трикутника, опущена на сторону.
В рівнобедреному трикутнику (трикутник в якому дві сторони конгруентні) висота проведена до неконгруентної сторони ділить цю сторону на дві рівні частини. В прямокутному трикутнику висота опущена на гіпотенузу ділить її на два відрізки, нехай це буде p і q. Якщо ми позначимо довжину висоти літерою h то отримаємо співвідношення:Три висоти перетинаються в одній точці, яка називається ортоцентром трикутника. Ортоцентр лежить всередині трикутника (і відповідно всі основи перпендикулярів лежать в трикутнику) тоді і тільки тоді, якщо трикутник не тупокутний (в ньому жоден з внутрішніх кутів не більший за прямий кут). Дивіться також ортоцентрична система. 







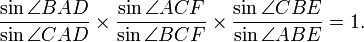



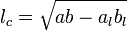


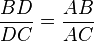

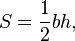
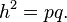
Немає коментарів:
Дописати коментар