Нерівність для сторін трикутника
Для
будь-яких
трьох
точок А, В, С,
що
не лежать на одній прямій
виконуються
нерівності:
АВ<BC+AC
АC<BC+AB
CВ<BA+AC.
Нерівність для медіан трикутника
Будь-яка
медіана
трикутника АВС
трикутника АВС
менше
півсуми сторін,
між якими вона лежить:
між якими вона лежить:
0,5(a+b-c)<mc<0,5(b+c)
0,5(a+c-b)<mb<0,5(a+c)
0,5(b+c-a)<ma<0,5(a+c)
Довести
нерівності:
(a+b-c)(c-b+a)(c-a-b) =<abc,
a2b(a-b) + b2c(b-c) + c2a(c-a) >
=0,
a(b-c)2 +b(c-a)2 +c(a-b)2 +4abc
> a3+b3+c3,
якщо
додатні усі дійсні змінні та a, b, c- сторони
трикутника.
Заглянь на цю сторінку:
ЗАДАЧИ ПО ГЕОМЕТРИИ
В данном разделе представлены задачи по геометрии. [Карточка ресурса]
ГЕОМЕТРИЧЕСКИЕ НЕРАВЕНСТВА
Нерівності математичних олімпіад.
Каталог класичних нерівностей:
Осмислення способів доведення нерівностей.
На практиці математики використовують для доведення різні способи:
- за визначенням(віднімання більшого від меншого);
- способом додавання лівих та правих частин класичних нерівностей;
- способом від супротивного;
- методом математичної індукції;
- штучні способи;
- синтез декількох способів доведення.
Означення
Для довільних дійсних чисел виконується нерівність
Доведення
перенесемо всі члени в ліву частину і помножино на 2:
виділимо повні квадрати:
Очевидно що рівність досягається тоді і тільки тоді, коли всі три числа рівні.
Завдання для самостійного опрацювання
Завдання для самостійного опрацювання
1.Довести нерівність
x3(1+y)-1(1+z)-1 + y3(1+x)-1(1+z)-1 +z3(1+y)-1(1+x)-1 >=0,75,
якщо додатні усі дійсні змінні та xyz=1
2.Довести нерівність
a2(a+2b3)-1+ b2(b+2c3)-1 + c2(a+2a3)-1>=1,
якщо додатні усі дійсні змінні та a + b + c = 3.
3.Довести нерівність
(1+a) (1+ b2)-1 +(1+b) (1+ c2)-1 +(1+c) (1+ a2)-1>=3,
якщо додатні усі дійсні змінні та a + b + c = 3.
4.Довести нерівність
(z+y+x)0,5 >= (x-1)0,5 + (y-1)0,5 + (z-1)0,5
якщо усі дійсні змінні не менше 1 та x -1 + y -1 +z-1 = 2.
5.Довести нерівність
a3(a3+b3 +abc)-1+ b3(a3+c3 +abc)-1 + c3(a3+c3+abc)-1>=1,
якщо додатні усі дійсні змінні.
6.Довести нерівність
(a2+1) (b2+1) (c2+1) >=8,
якщо додатні усі дійсні змінні та ab+ cb + ac = 3.
Каталог класичних нерівностей:
1. Сума двох взаємно обернених додатних чисел не менше двох, тобто якщо для чисел a∙b=1, тоді
a/b+b/a>=2
Сума двох взаємно обернених недодатних чисел не менше двох, тобто якщо для чисел a∙b= -1, тоді
a/b+b/a=<-2
2. Для невід’ємних n:
1/n+ n>=2
3. Якщо для невід’ємних чисел a∙b=1, тоді
(a+b)>=2.
4. Якщо для невід’ємних m чисел a∙b∙c∙d∙e∙…∙f=1, тоді
(a+b+c+d+e+…+f)> =m.
5. Для довільного а вірно:
а2>=0.
6. Для довільної послідовності чисел аі вірно:
а12+ а22 +а32+ …+аn2>=0
7. Для додатного числа а>0 та від’ємного дискримінанта: b2-4aс<0 завждивиконується квадратна нерівність:
ax2+bx+c>0.
8. Для від’ємного числа а<0 та від’ємного дискримінанта: b2-4aс<0 завждивиконується квадратна нерівність:
ax2+bx+c<0.
Яку нерівність можна використати для доведення нерівності Несбіта:
Із нерівностей Коші-Буняковського і трьох квадратів отримуємо:

- з чого негайно слідує нерівність Несбіта.
- 1. Довести, що для будь-яких чиселa2+b2+c2>=ab+bc+ac.Вказівка. Додати окремо ліві та праві частини нерівностей:a2+b2 >= 2ab, с2+b2 >= 2сb, a2+с2 >= 2aс. Рівність досягається, якщо a=b=c.2.Довести, що для будь-яких чисел a, b, c, які мають однакові знаки:. a/b+b/c+ c/a>=33.Для додатних a, b дріб c+d/a+bлежить між дробами c/a таb/dДовести.4.Довести, що невід’ємних трьох дійсних чисел виконується нерівність:. ab/c+ac/b+ cb/a>=3
-
Визначення
Через граничний перехід довизначаються такі величини:
Часткові випадки
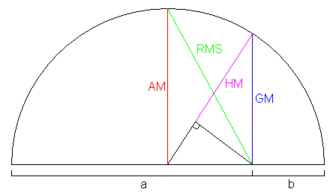
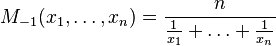 — середнє гармонійне (HM),
— середнє гармонійне (HM),![M_0(x_1,\dots,x_n) = \sqrt[n]{x_1\cdot\dots\cdot x_n}](http://upload.wikimedia.org/math/0/5/e/05e40c7677e45396178661635deb0605.png) — середнє геометричне (GM),
— середнє геометричне (GM), — середнє арифметичне (AM),
— середнє арифметичне (AM), — середнє квадратичне (RMS).
— середнє квадратичне (RMS).









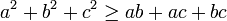
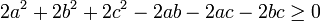







 —
— 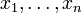 як:
як:
![M_0(x_1, \ldots, x_n) = \lim_{p\to 0} M_p(x_1, \ldots, x_n) = \sqrt[n]{x_1\cdot\dots\cdot x_n}](http://upload.wikimedia.org/math/e/a/2/ea27c29d98bebb5c3ee9310727773a0a.png)

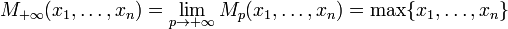
чівоооооооооооооо
ВідповістиВидалити