Рівняння Пелля — діофантове рівняння вигляду:
де  — додатне ціле число, що не є точним квадратом цілого числа. Рівняння Пелля є класом діофантових рівнянь другого степеня.
— додатне ціле число, що не є точним квадратом цілого числа. Рівняння Пелля є класом діофантових рівнянь другого степеня.
 — додатне ціле число, що не є точним квадратом цілого числа. Рівняння Пелля є класом діофантових рівнянь другого степеня.
— додатне ціле число, що не є точним квадратом цілого числа. Рівняння Пелля є класом діофантових рівнянь другого степеня.
Доведено, що при кожному такому значенні  рівняння має задану нескінченну послідовність розв'язків. Одним із застосувань теорії рівняння Пелля є наближення ірраціонального числа
рівняння має задану нескінченну послідовність розв'язків. Одним із застосувань теорії рівняння Пелля є наближення ірраціонального числа  раціональними з якомога меншою похибкою.
раціональними з якомога меншою похибкою.
 рівняння має задану нескінченну послідовність розв'язків. Одним із застосувань теорії рівняння Пелля є наближення ірраціонального числа
рівняння має задану нескінченну послідовність розв'язків. Одним із застосувань теорії рівняння Пелля є наближення ірраціонального числа  раціональними з якомога меншою похибкою.
раціональними з якомога меншою похибкою.Розв'язки
Рівняння Пелля для довільного n має пару тривіальних розв'язків 

У випадку коли n не є точним квадратом існує нескінченна кількість розв'язків.
Якщо  — наближені дроби розкладу
— наближені дроби розкладу 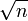 у ланцюговий дріб з періодом k, то додатні розв'язки рівняння Пелля мають вигляд:
у ланцюговий дріб з періодом k, то додатні розв'язки рівняння Пелля мають вигляд:
 — наближені дроби розкладу
— наближені дроби розкладу 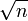 у ланцюговий дріб з періодом k, то додатні розв'язки рівняння Пелля мають вигляд:
у ланцюговий дріб з періодом k, то додатні розв'язки рівняння Пелля мають вигляд:
де m — будь-яке натуральне число таке, що km є парним.
Всі додатні розв'язки рівняння Пелля можна одержати з формули:
де k — будь-яке ціле, а (х1, у1) — розв'язок з найменшими додатними значеннями невідомих.
Еквівалентно розв'язки можна знайти із рекурентних співвідношень:
Зв'язок з алгебраїчною теорією чисел
Пара (x, у) є розв'язком рівняння Пелля тоді і тільки тоді, коли норма числа 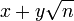 у розширенні
у розширенні  поля
поля 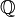 рівна одиниці:
рівна одиниці:
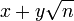 у розширенні
у розширенні  поля
поля 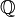 рівна одиниці:
рівна одиниці:
Зокрема, рішенню відповідає оборотний елемент кільця ![Z[\sqrt{n}]](http://upload.wikimedia.org/math/f/8/2/f820b1e5d6a1f68636b487465cfe18db.png) . Тому, зважаючи на мультиплікативність норми, розв'язки можна множити і ділити: розв'язкам
. Тому, зважаючи на мультиплікативність норми, розв'язки можна множити і ділити: розв'язкам 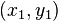 і
і 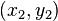 можна поставити у відповідність розв'язки
можна поставити у відповідність розв'язки
![Z[\sqrt{n}]](http://upload.wikimedia.org/math/f/8/2/f820b1e5d6a1f68636b487465cfe18db.png) . Тому, зважаючи на мультиплікативність норми, розв'язки можна множити і ділити: розв'язкам
. Тому, зважаючи на мультиплікативність норми, розв'язки можна множити і ділити: розв'язкам 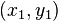 і
і 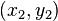 можна поставити у відповідність розв'язки
можна поставити у відповідність розв'язкиПриклад[ред. • ред. код]
Для рівняння  найменшим додатним розв'язком буде пара чисел
найменшим додатним розв'язком буде пара чисел 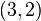 . Всі додатні розв'язки відповідно можна одержати за допомогою формули:
. Всі додатні розв'язки відповідно можна одержати за допомогою формули:
 найменшим додатним розв'язком буде пара чисел
найменшим додатним розв'язком буде пара чисел 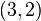 . Всі додатні розв'язки відповідно можна одержати за допомогою формули:
. Всі додатні розв'язки відповідно можна одержати за допомогою формули:
Якщо  — розв'язки, то розв'язками також будуть числа
— розв'язки, то розв'язками також будуть числа 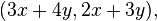 які можна визначити як
які можна визначити як  згідно з уведеним вище добутком.
згідно з уведеним вище добутком.
 — розв'язки, то розв'язками також будуть числа
— розв'язки, то розв'язками також будуть числа 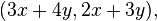 які можна визначити як
які можна визначити як  згідно з уведеним вище добутком.
згідно з уведеним вище добутком.
Дійсно:
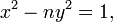


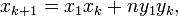

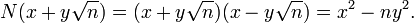


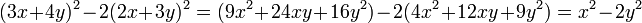
Немає коментарів:
Дописати коментар