Числа Піфагора (піфагорова трійка) складаються з трьох додатніх цілих чисел a, b і c, таких що a2 + b2 = c2. Ці числа зазвичай записують в такому вигляді (a, b, c), і найвідоміший приклад (3, 4, 5). Якщо (a, b, c) числа Піфагора, тоді і (ka, kb, kc) також для будь-якого цілого додатнього k. Примітивними Піфагоровими числами називають взаємно прості a, b й c.
Назву свою числа отримали через теорему Піфагора, для якої ці числа є розв’язком. Але не всі розв’язки теореми є Піфагоровими числами. Наприклад, трикутник зі сторонами a = b = 1 і c = √2 прямокутний, але (1, 1, √2) не є піфагоровими числами, тому що √2 — не ціле число. Більше того, 1 і √2 не мають цілого спільного кратного, тому що √2 ірраціональне число. Для c ≤ 100 є лише 16 примітивних Піфагорових трійок:
| ( 3, 4, 5) | ( 5, 12, 13) | ( 7, 24, 25) | ( 8, 15, 17) |
| ( 9, 40, 41) | (11, 60, 61) | (12, 35, 37) | (13, 84, 85) |
| (16, 63, 65) | (20, 21, 29) | (28, 45, 53) | (33, 56, 65) |
| (36, 77, 85) | (39, 80, 89) | (48, 55, 73) | (65, 72, 97) |
Загальні формули[ред. • ред. код]
За допомогою простих арифметичних обчислень неважко перевірити, що для довільних цілих m>n числа
є числами Піфагора. Вони будуть примітивними, якщо й тільки якщо m і n взаємно прості й одне з них парне (якщо б обидва були непарними, тоді числа a, b і c були б парними, а значить, трійка не була б примітивною). З іншого боку можна довести, що всі примітивні числа Піфагора можна задати подібним чином. Справді, нехай a,b,c - деякі примітивні числа Піфагора. Вочевидь, два з них мають бути непарними, а одне - парним. Доведемо, що випадок, коли a,b- непарні, а c - парне неможливий. Справді, якщо c є парним, то c2 ділиться на 4, тоді як a2 + b2 =(2p+1)2 + (2q+1)2 =4p2+4p+1+4q2+4q+1 при діленні на 4 дає в остачі 2. Отже, припустимо, що a,c- непарні, а b - парне. Записавши a2 - c2 = b2 і враховуючи a2 - c2 = (a+с)(a-с) ділячи на 4 остаточно, одержуємо:
У попередній формулі множники в лівій частині є взаємно простими. Інакше їх спільний дільник був би спільним дільником і для a,c, а значить і для b, що неможливо. Оскільки два множники взаємно прості, а їх добуток є квадратом цілого, то кожне з цих чисел є квадратом цілого.
Поклавши, що:
і виразивши a,b,c через m,n одержуємо необхідні формули.
Теоре́ма Піфаго́ра - одна із засадничих теорем
евклідової геометрії, котра встановлює співвідношення між сторонами прямокутного трикутника. Вважається, що вона доведена грецьким математиком Піфагором, на
честь котрого вона названа (є й інші версії, зокрема альтернативна думка, що ця
теорема у загальному вигляді була сформульована математиком-піфагорійцем Гіппасом).
Довідник з геометрії прямокутного трикутника
Властивості
прямокутних трикутників
1.У прямокутному
трикутнику сума гострих кутів рівна 900.
2.Рівнобедрений
прямокутний трикутник має рівні гострі кути по 450.
3.У прямокутному
трикутнику напроти кута 300 лежить катет, що дорівнює половині
гіпотенузи.
4.Площа
прямокутного трикутника рівна половині добутку
його катетів.
5.У прямокутному
трикутнику медіана, що проведена до гіпотенузи рівна половині гіпотенузи.
6.У прямокутному
трикутнику кут між бісектрисами гострих кутів рівний 1350.
7.У прямокутному
трикутнику бісектриса прямого кута ділить кут між медіаною та висотою, що
проведені з вершини прямого кута навпіл.
8.У прямокутному
трикутнику висота, що проведена з прямого кута розділяє трикутник його на два
прямокутних трикутники, у яких рівні кути.
9.У прямокутному
трикутнику медіана, що проведена з прямого кута розділяє трикутник його на два
необов’язково рівних рівнобедрених трикутники..
10. У прямокутному
трикутнику кут між медіаною та висотою, що проведені з вершини прямого кута
дорівнює різниці гострих кутів трикутника.
11. У прямокутному
трикутнику кут між медіаною та бісектрисою, що проведені з вершини прямого кута
дорівнює піврізниці гострих кутів трикутника.
12. У прямокутному
трикутнику кут між бісектрисою та висотою, що проведені з вершини прямого кута
дорівнює піврізниці гострих кутів трикутника.
13. У прямокутному
трикутнику центр описаного кола лежить в
центрі гіпотенузи, а радіус цього кола дорівнює
половині гіпотенузи.
14. У прямокутному
трикутнику центр вписаного кола лежить в
точці перетину двох бісектрис, а радіус цього кола дорівнює половині сумі катетів без гіпотенузи.
15. У прямокутному
трикутнику квадрат висоти, що проведена до гіпотенузи, рівний добутку проекцій катетів на
гіпотенузу.
16. У прямокутному
трикутнику квадрат катета рівний добутку довжини проекції цього катета на
гіпотенузу на довжину гіпотенузи.
17. У прямокутному
трикутнику точка перетину висот лежить у
вершині прямого кута.
18. У прямокутному
трикутнику квадрат гіпотенузи дорівнює сумі квадратів його катетів.
19. У прямокутному
трикутнику площа кола побудованого на гіпотенузі, як на діаметрі, дорівнює сумі
площ кіл, що побудовані на його катетах, як на діаметрах.
20. У прямокутному
трикутнику площа квадрату побудованого на гіпотенузі, як на стороні, дорівнює
сумі площ двох квадратів, що побудовані на його катетах, як на сторонах.
21. Прямокутний
трикутник можна розрізати на три тупокутних трикутники.
22. Прямокутний
трикутник можна розрізати на гострокутні трикутники.
23. Прямокутний
трикутник можна розрізати на три трапеції.
24. Прямокутний трикутник
не можна розрізати на паралелограми.
25. Прямокутний
трикутник можна розрізати на три чотирикутники, діагоналі яких
перпендикулярні..
26. У прямокутному
трикутнику , якщо гострі кути відносяться, як 1:3, то бісектриса прямого кута
рівна одному з катетів цього трикутника.
27. У прямокутному
трикутнику , якщо гострі кути відносяться, як 1:2, то медіана прямого кута
рівна одному з катетів цього трикутника.
28. У прямокутному
трикутнику, якщо висота, проведена на гіпотенузу, ділить її на відрізки,
різниця яких рівна одному з катетів трикутника, то гострі кути відносяться, як
1:2.
29. У прямокутному
трикутнику, якщо сторони утворюють арифметичну прогресію, то різниця цієї
прогресії рівна радіусу вписаного в цей трикутник кола.
30. Висота,
що виходить з вершини прямого кута трикутника, рівна добутку катетів,
поділеному на гіпотенузу.
31. Відношення
проекцій катетів на гіпотенузу дорівнює відношенню квадратів катетів.
32. Якщо
сторона трикутника являється діаметром його описаного кола, то протилежний їй
кут – прямий, тобто трикутник прямокутний.
33. Якщо квадрат найдовшої сторони трикутника
рівний сумі квадратів двох інших сторін цього трикутника, то трикутник
прямокутний.
34. Теорема
Гіппократа: Сума площ „місяців”, що лежать між дугою напівкола, яке побудоване
на гіпотенузі як на діаметрі, і дугами кіл, що побудовані на катетах як на
діаметрах, дорівнює площі даного трикутника.
35. У прямокутному трикутнику з гострим кутом 300 найменша
висота ділить гіпотенузу у
відношенні 3:1, починаючи з вершини меншого кута.
36. У прямокутному трикутнику з гострим кутом 300 бісектриса середнього кута ділить середню
сторону у відношенні 1:2 починаючи від вершини прямого кута.
37. У прямокутному трикутнику з гострим кутом 300 найменша висота рівна половині більшого
катета.
38. У прямокутному трикутнику з гострим кутом 750 найменша висота рівна чверті гіпотенузи.
39. У прямокутному
трикутнику з гострим кутом 750 найменша висота рівна половині радіуса
описаного кола.
40. У прямокутному трикутнику з гострим кутом 150 найменша квадрат найменшої висоти рівний
половині площі трикутника.
41. У прямокутному трикутнику з гострим кутом 600 кожна сторона поділена точкою на дві
частини у відношенні 1:2, починаючи з
вершини більшого кута. Ці три точки поділу сторін утворюють правильний
трикутник, площа якого становить дві дев’ятих площі прямокутного трикутника. Ці
три точки поділу сторін є точками дотику вписаного кола в даний прямокутний
трикутник.
42. У прямокутному трикутнику з гострим кутом 600 найменша висота ділить бісектрису середнього
кута навпіл.
43. У прямокутному трикутнику з гострим кутом 600 найменша медіана перпендикулярна до бісектриси
середнього кута.
44. У прямокутному трикутнику з гострим кутом 600 бісектриса середнього кута ділить навпіл
найменшу медіану.
45. У прямокутному трикутнику найменша медіана ділить навпіл
площу цього трикутника.
46. У прямокутному трикутнику сторони можуть виражаюти
натуральними числами за формулами: а = m2 – n2; b = 2mn; c = m2
+ n2
.
47. b - с < a < b + с, с - а < b < с + а і а - b < с < а + b.
|
m/n
|
2
|
4
|
6
|
8
|
10
|
12
|
|
1
|
3, 4, 5
|
15, 8,17
|
35,12,37
|
63,16,65
|
99,20,101
|
143,24,145
|
|
3
|
5,12,13.
|
7, 24.25
|
-------------
|
55.48.73
|
91.60,109
|
--------------
|
|
5
|
21.20.29
|
9.40.41
|
11, 60, 61
|
38, 80, 89
|
-------------
|
169,120,119
|
|
7
|
45.28.53
|
33.56.65
|
13.84.85
|
15.112.113
|
51.140.149
|
95.169.193
|
|
9
|
77.36.85
|
65.72.97
|
------------
|
17.144.145
|
19.180.181
|
-------------
|
|
11
|
44.117.125
|
88.105.137
|
85.132.157
|
57.176.185
|
21.220.221
|
23.264.265
|
|
13
|
52.165.173
|
104.153.135
|
133.156.175
|
105.208.233
|
69.260.269
|
25.312.313
|
|
15
|
60.221.229
|
120.209.241
|
-----------
|
161.240.289
|
-------------
|
--------------
|
|
17
|
68.285.293
|
136.273.305
|
204.253.325
|
225.273.353
|
189.340.380
|
145.408.433
|
|
19
|
76.357.365
|
152.345.377
|
228.325.397
|
297.304.425
|
261.380.461
|
217.456.505
|
|
21
|
84.437.445
|
168.425.457
|
------------
|
366.377.505
|
341.420.541
|
--------------
|
|
23
|
92.525.533
|
184.513.540
|
276.493.565
|
368.468.593
|
429.460.629
|
385.552.673
|
|
25
|
100.621.629
|
200.609.641
|
589.300.661
|
400.561.689
|
-------------
|
481.600.769
|
Рівні трикутники
Два трикутники називають рівними якщо у них відповідно рівні три сторони
та відповідно рівні три кути.
Теорема 1 (перша
ознака рівності трикутників). Якщо дві сторони і кут між ними
одного трикутника дорівнюють відповідно двом сторонам і куту між ними другого трикутника то такі трикутники
рівні.
Теорема 2 (друга ознака рівності
трикутників) Якщо
сторона та прилеглі до неї кути одного трикутника
дорівнюють відповідно стороні та прилеглим до неї
кутам другого трикутника, то такі трикутники рівні.
Теорема 3
(третя ознака рівності трикутників) Якщо три сторони одного трикутника дорівнюють відповідно трьом сторонам другого трикутника, то такі трикутники рівні.
Властивості рівних трикутників
- У рівних трикутників всі відповідні
лінійні елементи(медіани, висоти,
бісектриси, середні лінії) рівні.
- У рівних трикутників проти рівних сторін лежать
рівні кути, а проти рівних кутів лежать рівні сторони..
- Рівні
трикутники можна переводити один в один за допомогою руху.
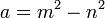
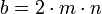




Немає коментарів:
Дописати коментар