Нера́венство Ю́нга в математике — элементарное неравенство, используемое в доказательстве неравенства Гёльдера. Является частным случаем более общего неравенства Юнга — Фенхеля.
Формулировка
Пусть  и
и  — сопряженные показатели (то есть такие числа, что
— сопряженные показатели (то есть такие числа, что  ). Тогда
). Тогда
 и
и  — сопряженные показатели (то есть такие числа, что
— сопряженные показатели (то есть такие числа, что  ). Тогда
). Тогда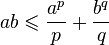 .
.
Доказательство[править | править вики-текст]
Для 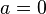 или
или 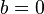 неравенство очевидно. Для
неравенство очевидно. Для  ,
, 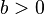 неравенство следует из выпуклости вверх (это свойство называется также вогнутостью)логарифмической функции: для любых
неравенство следует из выпуклости вверх (это свойство называется также вогнутостью)логарифмической функции: для любых  ,
, 
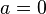 или
или 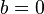 неравенство очевидно. Для
неравенство очевидно. Для  ,
, 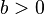 неравенство следует из выпуклости вверх (это свойство называется также вогнутостью)логарифмической функции: для любых
неравенство следует из выпуклости вверх (это свойство называется также вогнутостью)логарифмической функции: для любых  ,
, 
 .
.
Положив в этом неравенстве  получим, что
получим, что
 получим, что
получим, что ,
,
которое равносильно неравенству Юнга.
Альтернативный вариант
Доказательство, как частный случай неравенства Юнга-Фенхеля. Для скалярной функции неравенство Юнга-Фенхеля записывается в виде:
 ,
,
где 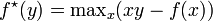 есть преобразование Лежандра от функции
есть преобразование Лежандра от функции  . Если положить
. Если положить  , то преобразование Лежандра в точке
, то преобразование Лежандра в точке 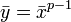 даёт
даёт
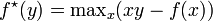 есть преобразование Лежандра от функции
есть преобразование Лежандра от функции  . Если положить
. Если положить  , то преобразование Лежандра в точке
, то преобразование Лежандра в точке 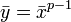 даёт
даёт ,
,
где 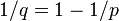 . Подставляя полученное в исходное неравенство получаем искомый результат.
. Подставляя полученное в исходное неравенство получаем искомый результат.
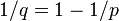 . Подставляя полученное в исходное неравенство получаем искомый результат.
. Подставляя полученное в исходное неравенство получаем искомый результат.Замечание
Равенство достигается в том и только том случае, когда  .
.
 .
.
Немає коментарів:
Дописати коментар