Вписанні 4-кутники і їх властивості
Означення 1. Колом, описаним навколо
чотирикутника, називають коло, що проходить через всі вершини чотирикутника
(рис.1). У цьому випадку чотирикутник називають чотирикутником, вписаним в
коло, або вписаним чотирикутником.

Рис.1
Чотирикутники
вписані в коло властивості
Теорема 1. Якщо чотирикутник вписаний в коло, то суми величин його протилежних
кутів дорівнюють 180 °.
Доведення. Кут ABC є вписаним кутом, що спирається на дугу кола ADC (рис.1).
Тому величина кута ABC дорівнює половині кутовий величини дуги ADC. Кут ADC є
вписаним кутом, що спирається на дугу ABC. Тому величина кута ADC дорівнює
половині кутовий величини дуги ABC. Звідси випливає, що сума величин кутів ABC
і ADC дорівнює половині кутовий величини дуги, що збігається з усім колом,
тобто дорівнює 180°.
Якщо розглянути кути BCD і BAD, то міркування буде аналогічним.
Теорема 1 доведена.
Теорема
2 (обернена до теоремі 1). Якщо у чотирикутника суми величин його протилежних
кутів дорівнюють 180°, то біля цього чотирикутника можна описати коло.
Доведення. Доведемо теорему 2 методом «від супротивного». З цією метою
розглянемо коло, що проходить через вершини A, B і С чотирикутника, і
припустимо, що це коло не проходить через вершину D. Доведемо це припущення до
протиріччя. Розглянемо спочатку випадок, коли точка D лежить всередині кола
(рис.2).

Рис.2
Продовжимо
відрізок CD за точку D до перетину з колом в точці E, і з'єднаємо
відрізком точку E з точкою (рис.2). Оскільки чотирикутник АВСЕ вписаний в коло,
то в силу теореми 1 сума величин кутів ABC і AEC дорівнює 180 °. При цьому сума
величин кутів ABC і ADC так само дорівнює 180 ° за умовою теореми 2. Звідси
випливає, що кут ADC дорівнює куту AEC. Виникає протиріччя, оскільки кут ADC є
зовнішнім кутом трикутника ADE і, звичайно ж, його величина більше, ніж
величина кута AEC, що не суміжного з ним.
Випадок, коли точка D виявляється лежить поза колом, розглядається аналогічно.
Теорема 2 доведена.
Перераховані в наступній таблиці властивості вписаних чотирикутників
безпосередньо випливають з теорем 1 і 2.
| Фігури | Рисунок | Властивість |
| Коло і паралелограм |  | Коло можна описати навколо паралелограма, якщо у нього усі кути прямі. |
| Коло і ромб |  | Коло можна описати навколо ромба, якщо у нього усі кути прямі. |
| Коло і трапеція |  | коло можна описати тільки навколо рівнобічної трапеції і навпаки якщо трапеція вписана, то вона рівнобічна. |
| Коло і дельтоїд |  | Окружность можно описать около дельтоида тогда и только тогда, когда дельтоид состоит из двух одинаковых прямоугольных треугольников. |
| Довільний вписаний 4-кутник |  | Площа довільного
вписаного
4-кутника можно знайти по формулі Брахмагупти:де a, b, c, d – довжини сторін 4-кутника, а p – півпериметр, т.е. |
Теорема Птолемея
Теорема Птолемея. Добуток діагоналей вписанного 4-кутника дорівнює сумі добутків протилежних сторін.
Доказательство. Рассмотрим произвольный четырёхугольник ABCD, вписанный в окружность (рис.3).

Рис.3
Докажем, что справедливо равенство:
Для этого выберем на диагонали AC точку E так, чтобы угол ABD был равен углу CBE (рис. 4).

Рис.4
Заметим, что треугольник ABD подобен треугольнику BCE. Действительно, у этих треугольников по два равных угла: угол ABD равен углу CBE (по построению точки E), угол ADB равен углуACB (эти углы являются вписанными углами, опирающимися на одну и ту же дугу). Следовательно,справедлива пропорция:
откуда вытекает равенство:
| (1) |
Заметим, что треугольник ABE подобен треугольнику BCD. Действительно, у этих треугольников по два равных угла: угол ABE равен углу DBC (углы ABD и EBC равны по построению, угол DBE – общий), угол BAC равен углу BDC (эти углы являются вписанными углами, опирающимися на одну и ту же дугу). Следовательно, справедлива пропорция:
откуда вытекает равенство:
| (2) |
Складывая равенства (1) и (2), получаем:
Теорема Птолемея доказана.
Неравенство Птолемея: Для любых точек  плоскости выполнено неравенство
плоскости выполнено неравенство
 плоскости выполнено неравенство
плоскости выполнено неравенство
причем равенство достигается тогда и только тогда, когда  (выпуклый) вписанный четырехугольник или точки ABCD лежат на одной прямой.
(выпуклый) вписанный четырехугольник или точки ABCD лежат на одной прямой.
 (выпуклый) вписанный четырехугольник или точки ABCD лежат на одной прямой.
(выпуклый) вписанный четырехугольник или точки ABCD лежат на одной прямой.Содержание
[убрать]Идеи доказательства[править | править вики-текст]
- Один из вариантов доказательства — применить инверсию относительно окружности с центром в точке A и неравенство треугольника для образов точек B, C, D.[1]
- Другой вариант (близкий к доказательству самого Птолемея, приведённому им в книге Альмагест) — ввести точку E такую, что
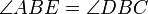 , а потом черезподобие треугольников.
, а потом черезподобие треугольников. - Неравенство также является следствием из соотношения Бретшнайдера.
Следствия[править | править вики-текст]
- Теорема Помпею.[2] Рассмотрим точку
 и правильный треугольник
и правильный треугольник 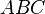 . Тогда из отрезков
. Тогда из отрезков  ,
,  и
и 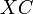 можно составить треугольник, причем этоттреугольник вырожденный тогда и только тогда, когда точка
можно составить треугольник, причем этоттреугольник вырожденный тогда и только тогда, когда точка  лежит на описанной окружности треугольника
лежит на описанной окружности треугольника 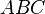 .
.
- Если AC — диаметр окружности, то теорема превращается в правило синуса суммы. Именно это следствие использовал Птолемей для составления таблицы синусов.
Вариации и обобщения[править | править вики-текст]
- Соотношение Бретшнайдера
- Неравенства Птолемея можно распространить и на шесть точек: если
 произвольные точки плоскости, то
произвольные точки плоскости, то
-
- причем равенство достигается тогда и только тогда, когда
 — вписанный шестиугольник.
— вписанный шестиугольник.
- Теорема Кэзи (обобщённая теорема Птолемея): Рассмотрим окружности
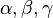 и
и  , касающиеся данной окружности в вершинах
, касающиеся данной окружности в вершинах  и
и  выпуклого четырехугольника
выпуклого четырехугольника  . Пусть
. Пусть 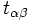 — длина общей касательной к окружностям
— длина общей касательной к окружностям  и
и  (внешней, если оба касания внутренние или внешние одновременно, и внутренней, если одно касание внутреннее, а другое внешнее);
(внешней, если оба касания внутренние или внешние одновременно, и внутренней, если одно касание внутреннее, а другое внешнее);  и т. д. определяются аналогично. Тогда
и т. д. определяются аналогично. Тогда
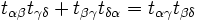 .
.


Немає коментарів:
Дописати коментар