Геометрична шкільна олімпіада для старшокласників

Поради учасникові олімпіади.

Прочитайте умови всіх  задач і помітьте, в якому порядку ви їх вирішуватимете. Врахуйте, що зазвичай завдання впорядковані за збільшенням їх труднощі.

Якщо умову, на ваш погляд, можна зрозуміти різними способами, то не вибирайте найзручніший для себе, а звертайтеся до черговому з питанням.

Якщо завдання зважилося дуже легко – це підозріло, можливо, ви неправильно зрозуміли умову або десь помилилися.

Якщо завдання не вирішується – спробуйте її спростити (узяти менші числа, розглянути окремі випадки і т.д.) або "порішать" її «від противного», або замінити числа буквами і т.д.

Якщо неясно, чи вірне деяке твердження, то намагайтеся його по черзі те доводити, то спростовувати (рада А. Н. Колмогорова).

Не зациклюйтеся на одному завданні: іноді відривайтеся від неї і оцінюйте свої можливості. Якщо є хоч невеликі успіхи, то можна продовжувати, а якщо думка ходить по кругу, то завдання краще залишити (хоч би на якийсь час).

Якщо втомилися, відверніться на декілька хвилин (подивіться на хмари або просто відпочиньте).

Вирішивши завдання, відразу оформляйте рішення. Це допоможе перевірити його правильність і звільнить увагу для інших завдань.

Кожен крок рішення треба формулювати, навіть якщо він здається очевидним.

УМОВИ ЗАДАЧ




1. У трикутнику АВС відрізки АF та СЕ перетинаються в точці D.  Дивись рисунок, на якому DM=MF; AE=EN=NB; BF =FC.  У якому відношенні ділиться відрізок АF  точкою D. У якому відношенні ділиться відрізок СЕ  точкою D.







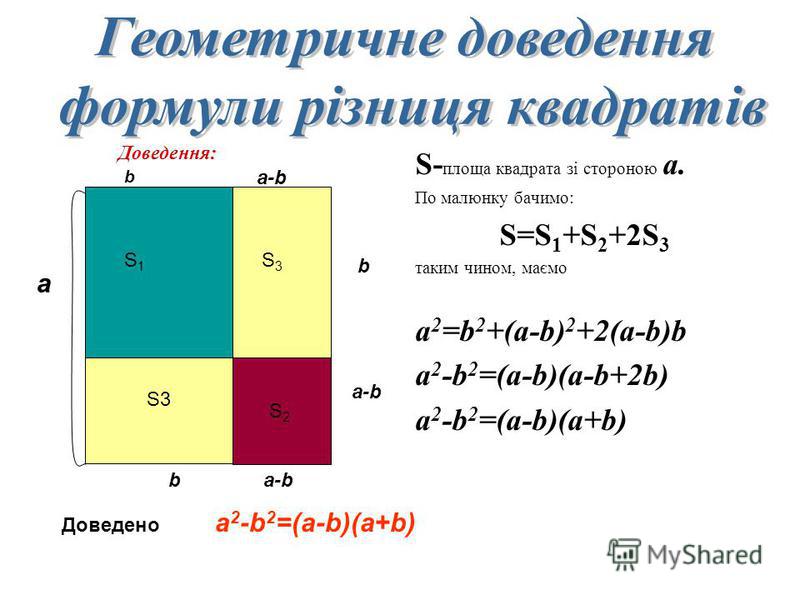
2.  У важно розгляньте  геометричне доведення для формули різниці квадратів. Проявіть кмітливість і самостійно складіть геометричне доведення квадрату суми трьох доданків, а саме (a+b+c)*(a+b+c)=?







3. Розгляньте рисунок. Відомі три  сторони прямокутного трикутника АВС: 3 см, 4 см, 5 см. У якому відношенні точки дотику вписаного кола в прямокутний трикутник АВС ділять кожну сторону?






4. Трикутники розглядаються на поверхні сфери. Які можуть бути величини трьох внутрішніх кутів правильного рівностороннього трикутника на поверхні сфері.


    





5. Правильні тіла. Скількома способами можна вписати правильний тетраедр в куб? Яке відношення ребер куба та вписаного в нього тетраедра? Яке відношення площ суми усіх граней куба і суми усіх граней вписаного в куб тетраедра? У скільки разів об'єм куба більший, ніж об'єм вписаного в нього тетраедра?