Задачі відкритої математичної олімпіади для учнів 5- х класів

      Задачі  першого етапу відкритої 

математичної олімпіади для учнів 5- х класів

1.      Із сірників складено невірну рівність: XXX + XIV = XV. 

Перекладіть одного сірника так, щоб рівність стала вірною.

2.      Знайдіть всі розв’язки рівняння ТИР + ТИР = КОРТ

(однакові цифри замінені однаковими літерами, а різні цифри – різними літерами).

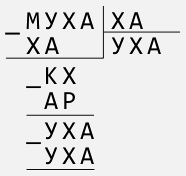
3.      Скільки семицифрових чисел можна скласти із цифр 0 та 1? 

Відповідь обґрунтувати.

4.       Розташувати на шаховій дошці 8 ферзів так, щоб вони не били один одного.                                 

( Ферзь ходить на будь-яку кількість клітинок 

по горизонталі, вертикалі та діагоналі).

   

5.       На дошці написали приклад на множення. 

Двійошник Михайлик виправив в

       прикладі 2 цифри. Отрималось  4 · 5 · 4 · 5 · 4 = 2247.   

Відновіть приклад  і поясніть як 

       ви це робили.

Задачі другого етапу відкритої 

математичної олімпіади для учнів 5 класів

6. Яка магічна сума  числового магічного квадрата "НАСІК" на сумах рядків та стовпців?
Складіть алгоритм утворення такого магічного квадрату із натуральних чисел від 1 до 64.

       

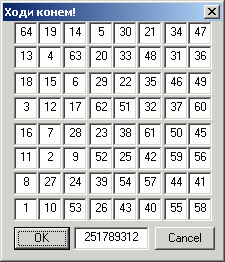
7. Обхід конем усієї шахової дошки

Якого кольору клітинки після парного ходу, де стоїть кінь?

Якого кольору клітинки після непарного ходу, де стоїть кінь?

Чому кольори початкової клітинки і кінцевої клітинки 

відрізняються під час ходу коня на шаховій дошці? 

8. Розгляньте шахові дошки А та Б для гри трьох учасників гри у шахи. Правила гри аналогічні тим, які використовують у звичайних класичних шахах? Як варто грати у шахи на трьох вам, як гравцеві,  що хоче тільки перемоги, домовляючись з одним із гравців чи самостійно без жодних домовлень? 

Шахова  дошка А

Шахова дошка Б.

9. Розгляньте шахову дошку  для гри 6-стьох учасників гри у шахи. Правила гри аналогічні тим, які використовують у звичайних класичних шахах? Як варто грати у шахи на 6-стьох вам, як гравцеві,  що хоче тільки перемоги, домовляючись з одним із а) 4-гравцями; б)3-гравцями; в) двома гравцями  чи самостійно - без жодних домовлень? 








10. Шахи на 6-кутній дошці з шестикутними клітинками.  Фігури ходять за правилами класичної гри в шахи. Укажіть найкращий перший хід білих і адекватну, найкращу відповідь чорних фігур! Поясніть і обгрунтуйте свою відповідь.




Третій етап відкритої математичної олімпіади в 5 класах

ВІДПОВІДІ:

1          XXX – XIV = XVI.

2                Ответ:  824 + 824 = 1648  и  849 + 849 = 1698. Очевидно, що  Т > 4 (інакше  сумма буде трицифровим числом) і парна цифра, так як вона остання цифра суми двох рівних чисел. Отримуємо 4 варіанти. 6«И»3 + 6«И»3 = 1«О»36, 6«И»8 + 6«И»8 = 1«О»86, 8«И»4 + 8«И»4 = 1«О»48 и 8«И»9 + 8«И»9 = 1«О»98. Тоді є два розв’язки:  824 + 824 = 1648  и  849 + 849 = 1698.

3          64. На першому місці може стояти тольки 1. На другому місці – або 0, або 1. Отже, для перших двох цифр – 2 варіанти. Для кожного із варіантів на третьому місці може стояти або 0, або 1. Тоді для перших трьох цифр – 4 варіанти. Аналогічно для перших чотирьох цифр – 8 варіантів, для 5 цифр – 16 варіантів, для 6 цифр – 32 варіанти, а для 7 цифр - 64.

4           Можна, наприклад так

5          Відповідь: 4 · 5 · 4 · 7 · 4 = 2240  або  4 · 7 · 4 · 5 · 4 = 2240.

В отриманому прикладі три співмножники парні, отже, у початковому прикладі хоча б один теж був парним. Тому і добуток  був парним числом , тобто остання цифра добутку була змінена была. Таким чином, зліва змінили  не більше однієї цифри. Тому, в початковому прикладі зліва були і п’ятірки, і четвірки, а закінчувався добуток на 0.

 Запис числа 4 · 5 · 4 · 5 · 4 = 1600 відрізняється від запису 2240 больше на одну цифру. З цього робимо висновок, що один із співмножників виправлений. Якщо виправлена четвірка, то добуток повинен  ділитися на 4 · 4 · 5 · 5 = 400, а 2240 на 400 не делиться, так що виправлялась одна із п’ятірок.