МАГІЧНІ КВАДРАТИ 3х3 НА СУМАХ

Задача.
Розмістити в таблиці 3х3, числа від 1 до 9 так, щоб виконувалась така умови: сума по усіх рядках, по усіх колонках, по двох діагоналях була однакова.
Відповідь.
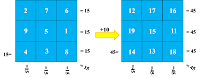
Зліва направо і зверху до низу числа мають розташуватися таким чином: 2, 7, 6, 9, 5, 1, 4, 3, 8.
Повного опису всіх можливих магічних квадратів не отримано і донині. Магічних квадратів 2х2 не існує. Існує магічний квадрат 3х3, а решта магічних квадратів 3х3 виходять з нього або поворотом навколо центру, або віддзеркаленням щодо однієї з його осей симетрії.

Нагадуємо способи утворення магічного квадрату 3х3.

Розташувати натуральні числа від 1 до 9 в магічний квадрат 3х3 можна 8 різними способами.

Знайти магічну суму для магічного квадрату 3х3: (1+2+3+4+5+6+7+8+9):3 = 45:3 =15.

Утворити суми з трьох доданків: 9+5+1 = 9+4+2 = 8+6+2 = 8+5+2 = 8+4+3 = 7+6+2 = 7+5+3 = 6+5+4 =15

У магічному квадраті 3х3 магічною постійною є число 15, отже, повинні бути рівні сумі трьох чисел по 8 напрямам: по 3 рядкам, 3 стовпцям і 2 діагоналям. Оскільки число, що стоїть в центрі, належить 1 рядку, 1 стовпцю і 2 діагоналям, воно входить в 4 з 8 трійок, що дають в сумі магічну постійну. Таке число тільки одне: це 5. Отже, число, що стоїть в центрі магічного квадрата 3х3, вже відоме: воно рівне 5.

Розглянемо число 9. Воно входить тільки в 2 трійки чисел: 9+5+1 = 9+4+2 = 15. Ми не можемо помістити його в кут магічного квадрату, оскільки кожна кутова клітка належить 3 трійкам: рядку, стовпцю і діагоналі. Отже, число 9 повинно стояти в клітинці, що межує тільки із однією стороною квадрата в її середині. Із-за симетрії квадрата байдуже, яку із сторін ми виберемо, тому пишемо 9 над числом 5, що стоїть в центральній клітці. По обидві сторони від дев'ятки у верхньому рядку ми можемо вписати тільки числа 2 і 4. Яке з цих двох чисел опиниться в правому верхньому кутку і яке в лівому, знову – таки не має значення, оскільки одне розташування чисел переходить в інше при дзеркальному віддзеркаленні. Решта кліток заповнюється автоматично.

4

9

2

3

5

7

8

1

6

Проведений нами спосіб побудови магічного квадрата 3х3 не єдиний. З іншими способами познайомимося трохи пізніше.

Запитання:

1. Що необхідно знайти для того щоб утворити магічний квадрат 3х3?

Відповідь: Спочатку треба знайти магічну суму для магічного квадрату 3х3:

(1+2+3+4+5+6+7+8+9):3 = 45:3 =15.

Потім утворити суми з трьох доданків:

9+5+1 = 9+4+2 = 8+6+2 = 8+5+2 = 8+4+3 = 7+6+2 = 7+5+3 = 6+5+4 = 15

2. Як утворити класичний магічний квадрат 3х3?

Відповідь: Для цього накресліть порожній клітинковий квадрат, розміром 3х3. Випішіть підряд натуральні числа : 1, 2,3,4, 5, 6, 7, 8, 9. Заповніть кожну клітинку якоюсь однією цифрою, використовуючи всі цифри, окрім 0, так , щоб сума трьох чисел, що розташовані по горизонталям, і сума трьох чисел, що розташовані по вертикалям, і сума трьох чисел, що розташовані по діагоналям була однакова.

Обговорення отриманих відповідей

Зрозуміло, що для того аби знайти число, яке рівне сумі чисел по рядкам, треба додати усі цифри та отримати 45. Якщо це число розділити на 3, то отримаємо 15. Отже, сума по горизонталях, по вертикалям, по діагоналям рівна 15. Середнє серед цифр 1, 2, 3, 4, 5, 6, 7, 8, 9 - це 5, тому воно повинно стояти в центральній клітинці.

Помітимо, що числа рівновіддаленні від числа 5 – це числа однакової парності і мають таку властивість: 1+ 9 =10, 2+8 =10, 3 + 7 =10, 4+ 6 = 10. Тоді в сусідній з нею клітинках повинні стояти непарні цифри.

Проблемне запитання: Чому в кутових клітинках магічного квадрату 3х3 повинні стояти тільки парні числа?

Відповідь: В кутових клітинках повинні стояти тільки парні числа, бо у противному випадку не утвориться магічний квадрат. Адже якщо цифра 7 і 9 опиняються або на одній діагоналі, або в одному стовпчику, тоді порушуються магічна сума на цій діагоналі або в цьому стовпчику(адже 9+7=16, що не рівне 15).

Знайшовши одне правильне розташування чисел в магічному квадраті можна отримати ще вісім таких квадратів за допомогою повороту навколо центральної клітинки.





БЛОК 2

МАГІЧНІ КВАДРАТИ
Означення. МАГІЧНИЙ КВАДРАТ – це квадратна клітинкова таблиця з цілими числами в клітинках, у якої суми чисел уздовж будь-якого рядка, будь-якого стовпця і будь-якою з двох головних діагоналей рівні одному і тому ж числу.

Магічний квадрат – математичний об’єкт старокитайського походження. Згідно легенді, за часів правління імператора Ю (близько 2200 до н.е.) з води Хуанхе (Жовтої річки) спливла священна черепаха, на панцирі якої були накреслені таємничі ієрогліфи і ці знаки відомі під назвою Ло-Шу і рівносильні магічному квадрату.

У 11 ст. про магічні квадрати дізналися в Індії, а потім в Японії, де в 16 ст. магічним квадратам була присвячена обширна література. Європейців з магічними квадратами познайомив в 15 ст. візантійський письменник Е.Мосхопулос. Першим квадратом, придуманим європейцем, вважається квадрат А.Дюрера, зображений на його знаменитій гравюрі «Меланхолія 1». Дата створення гравюри (1514) вказана числами, що стоять в двох центральних клітках нижнього рядка.

Магічним квадратам приписували різні містичні властивості. У 16 ст. Корнелій Генріх Агріппа побудував класичні магічні квадрати 3-го, 4-го, 5-го, 6-го, 7-го, 8-го і 9-го порядків, які були пов'язані з астрологією 7 планет. Існувало повір'я, що вигравійований на сріблі магічний квадрат захищає від чуми. Навіть сьогодні серед атрибутів європейських віщунів можна побачити магічні квадрати.



У 19 і 20 вв. інтерес до магічних квадратів спалахнув з новою силою. Їх сталі досліджувати за допомогою методів вищої алгебри і операційного числення. Кожен елемент магічного квадрата називається кліткою. Квадрат, сторона якого складається з n кліток, містить n?n кліток і називається магічним квадратом n-го порядку. У більшості класичних магічних квадратів використовуються перші n послідовних натуральних чисел.

Сума S чисел, що стоять в кожному рядку, кожному стовпці і на будь-якій діагоналі, називається постійною або магічною константою квадрата і рівна

S(n) = n(n² + 1):2.

Для квадрата 3-го порядку S(3) = 3(3²+1):2 = 15, 4-го порядку – S(4) = 4(4² + 1):2 = 34, 5-го порядку – S(5) = 5(5²+ 1):2 = 65.

Таблиця магічних констант для магічних квадратів: (n; S (n)): (3; 15),(4; 34),(5; 65),(6;111), (7; 175), (8; 260),(9; 369), (10; 505), (11; 671), (12; 870), (13; 1105), .... .

Дві діагоналі, що проходять через центр квадрата, називаються головними діагоналями.

Ламаною називається діагональ, яка, дійшовши до краю квадрата, продовжується паралельно першому відрізку від протилежного краю (таку діагональ утворюють заштриховані клітки на мал. ) Клітки, симетричні щодо центру квадрата, називаються кососиметричними.

Варто зазначити, що із збільшенням розмірів квадрата (числа клітинок) швидко росте і кількість можливих магічних квадратів такого розміру. Існує 3456 магічних квадратів порядка 4х4 і 275 305 224 магічних квадратів порядка 5х5. Причому, квадрати 5х5 були відомі ще в середні століття.

Мусульмани, наприклад, дуже благоговійно відносилися до таких квадратів з цифрою 1 в середині, вважаючи його символом єдності Аллаха.

Якщо в квадратну таблицю ( іноді математики говорять в «квадратну матрицю») nхn заноситься не строго послідовний натуральний ряд чисел, то даний магічний квадрат – нетрадиційний.