Звідки нестандартні задачі виникають?

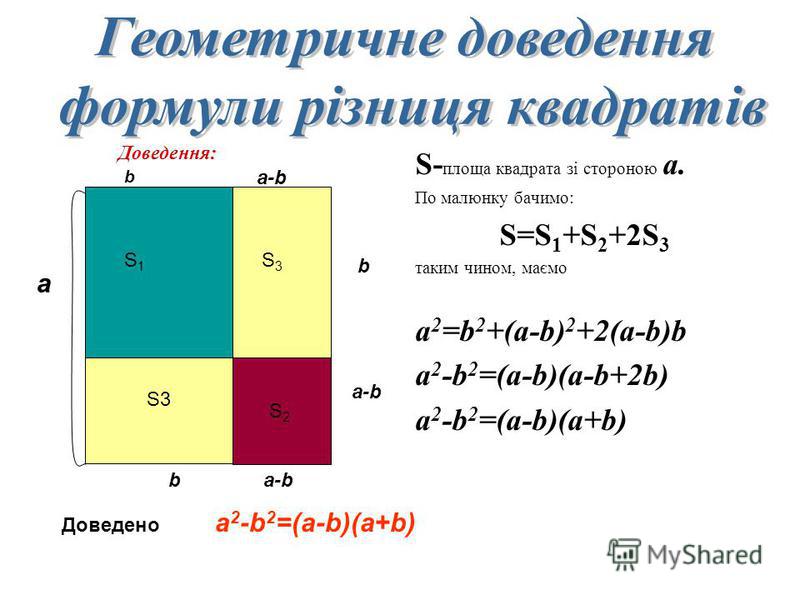
Заняття 1. Задачі на обведення фігур................................................

Заняття 2. Задачі на „сірниках”..........................................................

Заняття 3. Задачі на знаходження виграшної стратегії...................

Заняття 4. Задачі-ребуси.....................................................................

Заняття 5. Задачі на знаходження інваріантної властивості..........

Заняття 6. Задачі на розфарбування фігур........................................

Заняття 7. Задачі на розрізання клітинкових фігур..........................

Заняття 8. Задачі на знаходження „ у найгіршому випадку”...............

Заняття 9. Задачі комбінаторики........................................................

Заняття 10. Задачі на подільність чисел.............................................

Заняття 11. Задачі на порівняння числових велетнів.......................

Заняття 12. Задачі на дії з багатоцифровими числами.....................

Заняття 13. Задачі  на парність ............................................................

Заняття 14. Задачі логічного характеру..............................................

Заняття 15. Задачі на розв’язування рівнянь в цілих числах............

Заняття 16. Задачі на трикутниках.......................................................

Заняття 17. Задачі на чотирикутниках................................................

Заняття 18. Задачі на многокутниках..................................................

Заняття 19. Задачі на шахівниці..........................................................

Заняття 20. Задачі на конфігураціях фігур..........................................

Заняття 21. Задачі міжнародних математичних конкурсів................

Заняття 22. Задачі математичних КВК ................................................

Заняття 23. Задачі на математичних олімпіад......................................

Заняття 24. Задачі математичних боїв..................................................

Заняття 25. Задачі математичних рингів..............................................

Заняття 26. Задачі на розміщення фігур...............................................

Заняття 27. Задачі на використання графів...........................................

Заняття 28. Задачі на знаходження відсотків........................................

Заняття 29. Задачі на побудову.................................................................

Заняття 30. Задачі на прямокутному трикутнику....................................

Заняття 31. Задачі на дослідження властивостей чисел.......................

Заняття 32. Задачі на конструювання фігур .........................................

Заняття 33. Задачі на можливості „існування”.....................................

Заняття 34. Задачі на принцип Діріхле..................................................

Заняття 35. Задачі, що розв’язуються з кінця........................................

Заняття 36. Задачі математичного фольклору.......................................

Заняття 37. Задачі-софізми......................................................................

Заняття 38. Задачі на числових квадратах.............................................

Заняття 39. Задачі − головоломки............................................................

Заняття 40. Задачі відомих математиків................................................

Всего одна задача, с помощью которой проверяли логику у разведчиков

• Подписаться на AdMe
• Поделиться в Facebook
• Рассказать ВКонтакте

Это задача для самых смекалистых. Говорят, что ее давали на экзаменах будущим разведчикам.

Внимательно рассмотрите рисунок и ответьте на 13 вопросов.

1. Много ли времени осталось до новолуния?
2. Скоро ли наступит ночь?
3. Какое время года на рисунке?
4. В какую сторону течет река?
5. Судоходна ли она?
6. С какой скоростью движется поезд?
7. Давно ли прошел здесь предыдущий поезд?
8. Долго ли будет двигаться машина вдоль железной дороги?
9. К чему должен подготовиться водитель?
10. Есть ли здесь поблизости мост?
11. Есть ли в этом районе аэродром?
12. Легко ли машинистам встречных поездов тормозить состав?
13. Дует ли ветер?

Ответы:

1. Много ли времени осталось до новолуния?
Немного. Месяц старый (видно его отражение в воде).

2. Скоро ли наступит ночь?
Не скоро. Старый месяц виден на утренней заре.

3. Какое время года на рисунке?
Осень. По положению солнца легко сообразить, что журавли летят на юг.

4. В какую сторону течет река?
У рек, текущих в Северном полушарии, правый берег крутой. Значит, река течет от нас к горизонту.

5. Судоходна ли она?
Судоходна. Видны бакены.

6. С какой скоростью движется поезд?
Поезд стоит. Светится нижний глазок светофора — красный.

7. Давно ли прошел здесь предыдущий поезд?
Недавно. Он находится сейчас на ближайшем блокировочном участке.

8. Долго ли будет двигаться машина вдоль железной дороги?
Дорожный знак показывает, что впереди железнодорожный переезд.

9. К чему должен подготовиться водитель?
К торможению. Дорожный знак показывает, что впереди крутой спуск.

10. Есть ли здесь поблизости мост?
Вероятно, есть. Стоит знак, обязывающий машиниста закрыть поддувало.

11. Есть ли в этом районе аэродром?
В небе след самолета, сделавшего петлю. Фигуры высшего пилотажа разрешается делать только невдалеке от аэродромов.

12. Легко ли машинистам встречных поездов тормозить состав?
Знак возле железнодорожного пути показывает, что встречному поезду придется подниматься вверх по уклону. Затормозить его будет нетрудно.

13. Дует ли ветер?
Дует. Дым паровоза стелется, а ведь поезд, как мы знаем, неподвижен.

Источник: https://www.adme.ru/svoboda-kultura/vsego-odna-zadacha-s-pomoschyu-kotoroj-proveryali-logiku-u-razvedchikov-1021210/ © AdMe.ru

Сядьте поудобнее, возьмите листок бумаги, карандаш и приступайте к решению. Не торопитесь. Полученный ответ может обрадовать вас или привести в недоумение.

Вы готовы?

А вот и правильные ответы:

К сумме каждого уравнения прибавляем сумму предыдущего:

1 + 4 = 5
5 + 2 + 5 = 12
12 + 3 + 6 = 21
21 + 8 + 11 = 40

Таким образом, мы получаем один из правильных ответов - 40.

Используем формулу: a + b = a + a(b).

1 + (4 × 1) = 5
2 + (5 × 2) = 12
3 + (6 × 3) = 21
8 + (8 × 11) = 96

Так мы находим еще один правильный ответ - 96.

Источник: https://www.adme.ru/zhizn-nauka/eta-zadachka-pod-silu-tolko-odnomu-cheloveku-iz-tysyachi-1383015/ © AdMe.ru

На компьютерных курсах иногда приводят загадку, которую может разгадать человек, но не может пока разгадать ни одна машина. Вот она.

Сколько лет трем сестрам, если:

• Умножение их возрастов дает число 36.
• Сложение их возрастов дает 13.
• Старшая — блондинка.

Уже догадались?

Умножение их возрастов дает 36, то есть это одна из восьми следующих комбинаций:

36 = 2 × 3 × 6, сложение этих цифр дает число 11.

36 = 2 × 2 × 9, сложение этих цифр дает число 13.

36 = 4 × 9 × 1, сложение этих цифр дает число 14.

36 = 4 × 3 × 3, сложение этих цифр дает число 10.

36 = 18 × 2 × 1, сложение этих цифр дает число 21.

36 = 12 × 3 × 1, сложение этих цифр дает число 16.

36 = 6 × 6 × 1, сложение этих цифр дает число 13.

36 = 36 × 1 × 1, сложение этих цифр дает число 38.

Остается два варианта ответа, поскольку 2 + 2 + 9 равно 13, и 6 + 6 + 1 - тоже. Замечание: "Старшая - блондинка" - позволяет узнать о том, что есть старшая дочь, не имеющая близнеца. Итак, нам подходит только первая формула. Решение: три сестры - девяти лет старшая и два близнеца по два года.

Источник: https://www.adme.ru/zhizn-nauka/smozhete-li-vy-razgadat-zagadku-kotoraya-ne-pod-silu-kompyuteru-1381715/ © AdMe.ru

Задачі відкритої математичної олімпіади для учнів 6 х класів

                          Задачі відкритої математичної олімпіади для учнів 6 х класів

1.Чи можна записати 7 послідовних натуральних чисел так, щоб всього при цьому було записано а)18; б)28 цифр.

2.Знайти всі розв’язки ребусів, в якому однаковими буквами позначені однакові цифри, а різними – різні:

  

  3.На дошці написали приклад на множення. Двіюшник Михайлик виправив в  прикладі 2 цифри. Отрималось:  4 · 5 · 4 · 5 · 4 = 2247. Відновіть приклад і поясніть як ви це робили.
4.Розташувати на шаховій дошці 8 ферзів так, щоб вони не били один одного. ( Ферзь ходить на будь-яку кількість клітинок по горизонталі, вертикалі та діагоналі).

5.Пакет  самого чистого в світі кефіру  коштує 10 грн, причому кефір на 9 грн дорожчий за порожній пакет. Скільки коштує порожній пакет?


6.1 Знайти ціну кожного фрукту
6.1.  


6.2 Знайти ціну кожного автомобіля
.    


Зразок:

Геометрична шкільна олімпіада для старшокласників

Поради учасникові олімпіади.

Прочитайте умови всіх  задач і помітьте, в якому порядку ви їх вирішуватимете. Врахуйте, що зазвичай завдання впорядковані за збільшенням їх труднощі.

Якщо умову, на ваш погляд, можна зрозуміти різними способами, то не вибирайте найзручніший для себе, а звертайтеся до черговому з питанням.

Якщо завдання зважилося дуже легко – це підозріло, можливо, ви неправильно зрозуміли умову або десь помилилися.

Якщо завдання не вирішується – спробуйте її спростити (узяти менші числа, розглянути окремі випадки і т.д.) або "порішать" її «від противного», або замінити числа буквами і т.д.

Якщо неясно, чи вірне деяке твердження, то намагайтеся його по черзі те доводити, то спростовувати (рада А. Н. Колмогорова).

Не зациклюйтеся на одному завданні: іноді відривайтеся від неї і оцінюйте свої можливості. Якщо є хоч невеликі успіхи, то можна продовжувати, а якщо думка ходить по кругу, то завдання краще залишити (хоч би на якийсь час).

Якщо втомилися, відверніться на декілька хвилин (подивіться на хмари або просто відпочиньте).

Вирішивши завдання, відразу оформляйте рішення. Це допоможе перевірити його правильність і звільнить увагу для інших завдань.

Кожен крок рішення треба формулювати, навіть якщо він здається очевидним.

УМОВИ ЗАДАЧ




1. У трикутнику АВС відрізки АF та СЕ перетинаються в точці D.  Дивись рисунок, на якому DM=MF; AE=EN=NB; BF =FC.  У якому відношенні ділиться відрізок АF  точкою D. У якому відношенні ділиться відрізок СЕ  точкою D.







2.  У важно розгляньте  геометричне доведення для формули різниці квадратів. Проявіть кмітливість і самостійно складіть геометричне доведення квадрату суми трьох доданків, а саме (a+b+c)*(a+b+c)=?







3. Розгляньте рисунок. Відомі три  сторони прямокутного трикутника АВС: 3 см, 4 см, 5 см. У якому відношенні точки дотику вписаного кола в прямокутний трикутник АВС ділять кожну сторону?






4. Трикутники розглядаються на поверхні сфери. Які можуть бути величини трьох внутрішніх кутів правильного рівностороннього трикутника на поверхні сфері.


    





5. Правильні тіла. Скількома способами можна вписати правильний тетраедр в куб? Яке відношення ребер куба та вписаного в нього тетраедра? Яке відношення площ суми усіх граней куба і суми усіх граней вписаного в куб тетраедра? У скільки разів об'єм куба більший, ніж об'єм вписаного в нього тетраедра?





 

Задачі відкритої математичної олімпіади для учнів 5- х класів

      Задачі  першого етапу відкритої 

математичної олімпіади для учнів 5- х класів

1.      Із сірників складено невірну рівність: XXX + XIV = XV. 

Перекладіть одного сірника так, щоб рівність стала вірною.

2.      Знайдіть всі розв’язки рівняння ТИР + ТИР = КОРТ

(однакові цифри замінені однаковими літерами, а різні цифри – різними літерами).

3.      Скільки семицифрових чисел можна скласти із цифр 0 та 1? 

Відповідь обґрунтувати.

4.       Розташувати на шаховій дошці 8 ферзів так, щоб вони не били один одного.                                 

( Ферзь ходить на будь-яку кількість клітинок 

по горизонталі, вертикалі та діагоналі).

   

5.       На дошці написали приклад на множення. 

Двійошник Михайлик виправив в

       прикладі 2 цифри. Отрималось  4 · 5 · 4 · 5 · 4 = 2247.   

Відновіть приклад  і поясніть як 

       ви це робили.

Задачі другого етапу відкритої 

математичної олімпіади для учнів 5 класів

6. Яка магічна сума  числового магічного квадрата "НАСІК" на сумах рядків та стовпців?
Складіть алгоритм утворення такого магічного квадрату із натуральних чисел від 1 до 64.

       

7. Обхід конем усієї шахової дошки

Якого кольору клітинки після парного ходу, де стоїть кінь?

Якого кольору клітинки після непарного ходу, де стоїть кінь?

Чому кольори початкової клітинки і кінцевої клітинки 

відрізняються під час ходу коня на шаховій дошці? 

8. Розгляньте шахові дошки А та Б для гри трьох учасників гри у шахи. Правила гри аналогічні тим, які використовують у звичайних класичних шахах? Як варто грати у шахи на трьох вам, як гравцеві,  що хоче тільки перемоги, домовляючись з одним із гравців чи самостійно без жодних домовлень? 

Шахова  дошка А

Шахова дошка Б.

9. Розгляньте шахову дошку  для гри 6-стьох учасників гри у шахи. Правила гри аналогічні тим, які використовують у звичайних класичних шахах? Як варто грати у шахи на 6-стьох вам, як гравцеві,  що хоче тільки перемоги, домовляючись з одним із а) 4-гравцями; б)3-гравцями; в) двома гравцями  чи самостійно - без жодних домовлень? 








10. Шахи на 6-кутній дошці з шестикутними клітинками.  Фігури ходять за правилами класичної гри в шахи. Укажіть найкращий перший хід білих і адекватну, найкращу відповідь чорних фігур! Поясніть і обгрунтуйте свою відповідь.




Третій етап відкритої математичної олімпіади в 5 класах

ВІДПОВІДІ:

1          XXX – XIV = XVI.

2                Ответ:  824 + 824 = 1648  и  849 + 849 = 1698. Очевидно, що  Т > 4 (інакше  сумма буде трицифровим числом) і парна цифра, так як вона остання цифра суми двох рівних чисел. Отримуємо 4 варіанти. 6«И»3 + 6«И»3 = 1«О»36, 6«И»8 + 6«И»8 = 1«О»86, 8«И»4 + 8«И»4 = 1«О»48 и 8«И»9 + 8«И»9 = 1«О»98. Тоді є два розв’язки:  824 + 824 = 1648  и  849 + 849 = 1698.

3          64. На першому місці може стояти тольки 1. На другому місці – або 0, або 1. Отже, для перших двох цифр – 2 варіанти. Для кожного із варіантів на третьому місці може стояти або 0, або 1. Тоді для перших трьох цифр – 4 варіанти. Аналогічно для перших чотирьох цифр – 8 варіантів, для 5 цифр – 16 варіантів, для 6 цифр – 32 варіанти, а для 7 цифр - 64.

4           Можна, наприклад так

5          Відповідь: 4 · 5 · 4 · 7 · 4 = 2240  або  4 · 7 · 4 · 5 · 4 = 2240.

В отриманому прикладі три співмножники парні, отже, у початковому прикладі хоча б один теж був парним. Тому і добуток  був парним числом , тобто остання цифра добутку була змінена была. Таким чином, зліва змінили  не більше однієї цифри. Тому, в початковому прикладі зліва були і п’ятірки, і четвірки, а закінчувався добуток на 0.

 Запис числа 4 · 5 · 4 · 5 · 4 = 1600 відрізняється від запису 2240 больше на одну цифру. З цього робимо висновок, що один із співмножників виправлений. Якщо виправлена четвірка, то добуток повинен  ділитися на 4 · 4 · 5 · 5 = 400, а 2240 на 400 не делиться, так що виправлялась одна із п’ятірок.