9 клас. ІІ етап математичної олімпіади

Другий етап Всеукраїнської олімпіади юних математиків 2012 р.
9 клас

*1*

В колі зі радіусом  R провели хорду і паралельно до неї дотичну. З кінців хорди на дотичну опустили перпендикуляри. Обчислити найбільш можливий периметр одержаного прямокутника.

 *2*

Доведіть, що серед 160 осіб знайдуться, принаймні, 4 особи, дні народження яких припадають на один і той самий тиждень високосного року, що починається  з понеділка?

*3* 

Через вершину С прямого кута трикутника ABC  проведено пряму CD, перпендикулярну до його площини. AD  = a,   BD  = b,   CD  = c. Знайти медіану СM трикутника ABC.   

*4*

У рівнобедреному трикутнику з кутом при вершині 36° проведено бісектрису кута при основі. Скільки нових рівнобедрених трикутників утворилося? Які вони мають кути?

 *5*

Розв´язати рівняння:

| x+4 |+ х = | 7 – x | - х

*6*

У прямокутному трикутнику один з кутів дорівнює 30°. Із середини гіпотенузи провели до неї перпендикуляр. Довести, що довжина відрізка цього перпендикуляра, який лежить усередині трикутника, дорівнює третині довжини більшого катета. 

                                   9 клас

1. Знайдіть кількість цілих розв’язків системи нерівностей
   
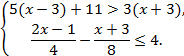
2. У рівнобедрений трикутник АВС з основою АС вписано коло, центр якою віддалений від вершини В трикутника на 51 см, а точка дотику ділить бічну сторону на відрізки, довжини яких відносяться як 8:9, рахуючи від вершини кута при основі. Знайдіть площу цього трикутника.
3. Два простих числа, які відрізняються на 2 називаємо простими числами-близнюками. (наприклад, 17 та 19). Знайдіть усі трійки послідовних простих чисел (х;у;z), таких, що x,y близнюки та у, z – також близнюки.
4. Усі точки площини пофарбовано в 4 кольори, причому кожен колір використовується. Чи обов’язково знайдеться пряма, що містить точки принаймні трьох різних кольорів?
5. Чотири відрізки з довжинами a,b,c,d такі, що з будь-яких трьох з них можна скласти трикутник. Довести, що з відрізків ab+cd, ac+bd і ad+bc також можна скласти трикутник.

На виконання завдань відводиться 4 години

Другий етап Всеукраїнської олімпіади юних математиків 2011 р.
Завдання

9 клас

ПЕРША ЧАСТИНА ЗАВДАНЬ

Записати правильну відповідь

1. У деякій державі 121 місто. Із кожного з них виходить однакова кількість доріг, що з'єднують його з деякими іншими містами. Яка кількість усіх доріг у державі?

А. 300.      Б. 440. В. 605.   Г. 330.

2. Знайдіть остачу від ділення на 5 числа 2005²⁰⁰⁷ + 2006²⁰⁰⁶ + 2007²⁰⁰⁵.

    А.0.        Б. 1.  В. 4.    Г. 3.

3. У трьох сусідніх вершинах правильного шестикутника розміщені фішки А, В і С. їх дозволяється переміщати в будь-якому порядку вздовж діагоналей у вільні вершини. При яко­му порядку проходження фішки не можуть знову потрапити в ті самі вершини, якщо у початко­вому положенні вони були розміщені у поряд­ ку АВС і рухалися за годинниковою стрілкою?

А. ВАС.      Б. СВА.     В. САВ.  Г. Можуть бути переставлені в будь-якому порядку.

4. Число (5-26 ^0,5)²⁰⁰⁷ має вигляд 0,000... .  Знайдіть кількість нулів після коми.

А. 27.     Б. 26.      В. Не більше 702.     Г. Не менше 2007.

5. Довжини всіх сторін трикутника не більші від одиниці. Чому дорівнює максимальна площа такого трикутника?

А. 0,5.  Б. 1.  В. 0,25  Г. Інша відповідь.

6. Продавець для збільшення прибутку змішав 5 літрів вершків з жирністю 30 %  з  4 літрами вершків з жирністю 15 % і долив туди ще літр чистої води. Скільки відсотків становить жирність отриманих «вершків»? А. 70%.     Б. 22,5%.      В. 15%.     Г. 21%.

7. Скількома способами можна зробити прямокутний отвір в аркуші паперу в клітинку роз­мірами 33 х 40 клітинок, якщо сторони отвору мають лежати на прямих, що розбивають аркуш на клітинки?

А. 367 536.     Б. 1178.   В. 735 072.    Г. 1248.

8. Учителька приготувала 27 однакових білих кубиків з довжиною ребра 10 см, маючи намір скласти з них білий куб з ребром 30 см. Яку най­меншу кількість граней маленьких кубиків має зафарбувати чорною фарбою Вовочка, щоб учи­телька не змогла здійснити свій намір?

А. 10.          Б. 13.   В. 11.      Г. 12.

9. Скільки розв'язків у натуральних числах має рівняння 200х + 1у = 2007 ?

А. 0.  Б. 1.   В. 2.            Г. Безліч.

10. Дев'ять робітників мають виготовити 50 виробів. Кожен виріб потрібно спочатку змонту­вати, а потім пофарбувати. Час монтажу — 20 хви­лин, час фарбування - 10 хвилин. Кого (малярів чи монтажників) і на скільки має бути більше, щоб виконати роботу в найкоротший час?

А Малярів на 1.         Б. Монтажників на 1.

В. Монтажників на 2. Г. Монтажників на 3.

11.     Прямокутний аркуш паперу з площею 5 розрізали на три трикутні шматки. Площа од­ного з них дорівнює півсумі площ двох інших шматків. Чому дорівнює площа найменшого шматка?

               А. 12      Б. 6.            В. 9.             Г . Інша   відповідь.

12. Придбали три книжки. Одна з них кош­тує третину всієї покупки, друга - кілька сьо­мих, а третя - 12 грн. Скільки гривень кошту­ють три книжки?

А. 252 грн      Б. 126 грн.     В. 250 грн.         Г. Інша   відповідь

13.     На картонну трубку з діаметром 3 см щільно намотали шар на шар 250 м стрічки тов­щиною 0,1 мм. Яким є діаметр отриманого ва­лика? (Виберіть найточніший результат.)

А. 186 мм.         Б. 153 мм.  В. 126 мм.        Г. 93 мм.

14.     Які з наступних тверджень еквівалентні, тобто одночасно істинні чи хибні?

1.Для кожного з учнів класу А знайдеться учень класу В нижчий за зростом.

2.Кожен із учнів класу В нижчий хоча б від одного з учнів класу А.

3.Найнижчий учень класу В нижчий від най­нижчого з учнів класу А.

4.Середній зріст учнів класу А більший від середнього зросту учнів класу В.

А. 1 і 2.     Б. 1 і 3.   В. 1 і 4.        Г. 2 і З.

15.     З кінцевих пунктів «Центр» і «Теремки» міського маршруту виїхали одночасно маршрут­ не таксі та автобус і їхали приблизно зі сталою швидкістю. Вони зустрілися на відстані 12 км  від «Центру». Після прибуття на кінцеві пунк­ти вони відразу ж вирушили у протилежних на­
прямах і цього разу зустрілися на відстані 16 км від кінцевої зупинки «Теремки». Якою є дов­жина маршруту?

А. 20 км.   Б. 24 км. В. 18 км.     Г. Визначити неможливо.

16.     Довжини сторін трикутника виражають­ ся цілими числами  l, т, п, де l<т<п . Скільки існує трикутників описаного виду, коли п = 9?

А. 9.  Б. 16.  В. 25.      Г. Інша відповідь.

ДРУГА ЧАСТИНА ЗАВДАНЬ

Записати обґрунтування задач

17.На сторонах трикутника як на діаметрах побудовано круги. Доведіть, що ці круги в су­купності цілком покривають трикутник.

18.Коник стрибає вздовж прямої, вибираючи напрям на ній для своїх стрибків навмання. Відо­мо, що довжина першого стрибка 1 м, кожний наступний стрибок удвічі довший від поперед­нього. Чи може коник після деякої кількості стрибків опинитися в початковій точці?

19.Чи можна обійти шахівницю розмірами 3x5 клітинок ходом шахового коня, побував­ши в кожній клітинці рівно один раз?

20.У деякому тайговому селищі від кожного з 17 будинків до деяких інших будинків прокладе­но лижню, причому від кожного будинку почи­наються 1, 3 чи 5 таких лижних стежок. Доведіть, що хоча б одна з них веде не до будинків селища.

21.Розв'яжіть у цілих числах рівняння  6х^г+1х²у + 2ху^г- 3у^г =12.

22.На площині дано точки А і В. Знайдіть гео­метричне місце точок площини, симетричних А відносно всіх прямих, що проходять через точку В.

23.Два брати віком 8 і 10 років одержали разом спадщину 84 тис. грн. Ці гроші поклали в банк, що нараховує 5 % на внесок щорічно. Кожна ди­тина одержить свою частину спадщини, досягши 21 року. За заповітом необхідно так поділити по­чатковий внесок, щоб у майбутньому обидві час­тини спадщини, округлені до 1 грн, були одна­кові. Як слід поділити 84 000 грн між братами?

24.Господарка розбила прямокутну ділянку шириною 5 м на 4 прямокутні грядки двома перпендикулярними доріжками. Причому пло­ща грядок, виділених під цибулю, моркву, бу­ряк, була не меншою від 5 м², а під капусту — не менша 10 м². Якою при цьому найменшою має бути довжина ділянки?

25.На дошці виписано числа 1,2, 3,..., 19,20. Дозволяється стерти будь-які два числа а і b і замінити їх числом аb+ а+b. Яке число може залишитися на дошці після 19 таких операцій?

26. Людина йде по шпалах залізничної колії. Максимальна довжина її кроку 0,8 м. Шпали покладено так, що на будь-якій стометровій ділянці — рівно 200 шпал. Відстань між шпала­ми не менша від 0,3 м і не більша від 0,6 м і може змінюватися в цих межах від шпали до шпали. При якому укладанні шпал людина зро­бить максимальну кількість кроків на 1 км шля­ху, а при якому - мінімальну?