10 клас. ІІ етап математичної олімпіади

Завдання ІІ етапу Всеукраїнської олімпіади з математики

10 клас

*1*

Обчислити

а³¹ – 74a³⁰ + 74a²⁹ - ...+74a¹⁷ – 74a¹⁶ + 73a¹⁵ + 15, якщо а = 73

*2*

В колі зі радіусом  R провели хорду і паралельно до неї дотичну. З кінців хорди на дотичну опустили перпендикуляри. Обчислити найбільш можливий периметр одержаного прямокутника.

*3*

Доведіть, що серед 160 осіб знайдуться, принаймні, 4 особи, дні народження яких припадають на один і той самий тиждень високосного року, що починається  з понеділка?

  *4*

Чи існує трикутник, сторони і кути якого  утворюють дві арифметичні прогресії?

*5*

 Через вершиу С прямого кута трикутника ABC  проведено пряму CD, перпендикулярну до його площини. AD  = a,   BD  = b,   CD  = c. Знайти медіану СM трикутника ABC.   

                                              10 клас

1. У рівнобедрений трикутник АВС з основою АС вписано коло, центр якого віддалений від вершини В трикутника на 51 см, а точка дотику ділить бічну сторону на відрізки, довжини яких відносяться як 8:9, рахуючи від вершини кута при основі. Знайдіть площу цього трикутника.
2. Функцію f(х) здано як суму нескінченно спадної геометричної прогресії:
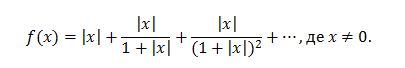               a) Знайдіть значення f(1)
               б) Побудуйте графік функції у = f(x).
3. Усі точки площини пофарбовано в 4 кольори, причому кожен колір використовується. Чи обов’язково знайдеться пряма, що містить точки принаймні трьох різних кольорів?
4. Чотири відрізки з довжинами a,b,c,d  такі, що з будь-яких трьох з них можна скласти трикутник. Довести, що з відрізків ab+cd, ac+bd і ad+bc також можна скласти трикутник.
5. У Кіри та Андрія разом 2012 цукерок. Кожну хвилину одночасно Андрій віддає Юрі половину кількості своїх цукерок, а Кіра – усі свої цукерки. Якщо в Андрія стає непарна кількість цукерок, то процес припиняється. Доведіть, що такий процес не може продовжуватися нескінченно довго.

На виконання завдань відводиться 4 години

10 клас

на виконання роботи надається 4 астрономічні години

1. Нехай х₁, х₂  - корені рівняння х² + ах + а = 2005. При якому значенні а  сума х₁² + х₂²  буде найменшою?

2. Розв’язати рівняння:

1+ а + а²+… + а^х = (1 + а) (1 + а²) (1 + а⁴) (1 + а⁸) (1 + а¹⁶) (1 + а³²)

, де х  - натуральне число.

3. Сума відстаней від внутрішньої точки паралелограма до прямих, на яких розташовані сторони паралелограма, дорівнює середньому арифметичному довжин його сторін. Знайти кути паралелограма.

4. Розв’язати рівняння  (х – {x})^0,5 - (х – [x])^0,5 = ²/₃  , де [x] - ціла частина числа x, а  {x}= x –[x] - дробова частина числа .

5. Цілі числа a, b, c  є послідовними членами геометричної прогресії. Довести, що рівняння aх² + bх - c = 0 не має цілих коренів.

На виконання роботи виділяється 4 години.

Використання записників і калькулятора не дозволяється.

Кожна задача оцінюється в 7 балів 

Загальні критерії оцінювання завдань наведено в таблиці.

7	Повне правильне розв’язання
6-7	Повне правильне розв’язання. Є невеликі недоліки, які в цілому не впливають на розв’язання.
5-6	Розв’язання в цілому вірне. Однак воно містить ряд помилок, або не                        розглянуті окремі випадки, але може стати правильним після невеликих                         виправлень або доповнень.
4	Правильно  розглянуто один з двох (більш складний) істотних випадків,                      або в задачі типу «оцінка-приклад» вірно отримана оцінка.
2-3	Доведені допоміжні твердження, що допомагають у розв’язанні задачі.
0-1	Розглянуто окремі важливі випадки за відсутності розв’язання (або при                       помилковому розв’язанні).
0	Розв’язання неправильне, просування відсутні. Розв’язання відсутнє.

 Не можна зменшувати кількість балів за те, що розв’язання занадто довге. Виправлення в роботі (закреслення раніше написаного тексту) також не є підставою для зняття балів. У той же час будь-як завгодно довгий текст розв’язання, що не містить корисних просувань, повинен бути оцінений в 0 балів.