11 клас. ІІ етап математетичної оліміпади

11 клас. ІІ етап математетичної оліміпади 2012 рік. 
Місто Дніпропетровськ.

11 клас

1. З точки А, віддаленої від площини γ на відстань  d, проведені до цієї площини похилі АВ і АС під кутом З0⁰ до площини. Їх проекції на площину γ утворюють кут в 120⁰. Знайдіть ВС.
2. При яких значеннях параметра а проміжок [0;a] містить не менше трьох коренів рівняння    
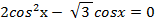
3. Відомо, що для деякої функції y=f(х) виконується рівність
   
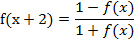     для усіх дійсних x.
   Доведіть, що ця функція періодична з періодом 4.
   Наведіть приклад такої функції.
4. Довести, що на заданій сфері можна виділити нескінчену множину точок, таку, що для будь-якої четвірки точок  A,B,C,D  з цієї множини відрізки
   АВ і СВ не перетинаються. (Сфера – множина усіх точок простору, віддалених від заданої точки на задану відстань).
5. У Кіри та Андрія разом m цукерок. Кожну хвилину одночасно Андрій віддає Кірі 1/k  від кількості своїх цукерок (тут к – деяке натуральне число), а Кіра – усі свої цукерки. Якщо в Андрія стає непарна кількість цукерок, то процес припиняється. Знайдіть усі m, для яких такий процес може продовжуватися нескінченно довго (вважається, що k задане).

На виконання завдань відводиться 4 години

Вінницька міська олімпіада юних математиків  2007 рік

11     клас

1.     Розв'язати рівняння:

2( х +  1/х)² + (х² +  1/х² )² – ( х +  1/х)²(х² +  1/х² ) = (х + 2)²

2.     Знайдіть найбільше натуральне число n таке, що число 2007!  ділиться на 2007ⁿ. (Нагадаємо, що 2007! = 1×2×3×... ×2005×2006×2007.)

3.      

3. Нехай a  і  b - такі гострі кути, що sіn a + sіn b < 1. Доведіть, що

                             sіn² a + sіn² b < sіn² (a+b).

4. Із точки, яка не лежить в площині, проведені до цієї площини перпендикуляр і три похилі, проекції яких на задану площину дорівнюють а, b  і   с.   Знайдіть   довжину   проведеного   перпендикуляра,   якщо   похилі утворюють з площиною кути, сума яких дорівнює 90 .

5. Дано 2007 однакових правильних п'ятикутників, при вершинах кожного із яких записані числа від 1 до 5, як показано на малюнку. П'ятикутники можна повертати і перевертати. Складіть усі 2007 п'ятикутників в стопку (вершина до вершини) так, щоб суми усіх чисел біля кожної вершини стопки були однаковими. А чи зможете ви зробити це, якщо п'ятикутників буде 2008?

На виконання роботи виділяється 4 години.

Використання записників і калькулятора не дозволяється.

Кожна задача оцінюється в 7 балів  

Загальні критерії оцінювання завдань наведено в таблиці.

7	Повне правильне розв’язання
6-7	Повне правильне розв’язання. Є невеликі недоліки, які в цілому не впливають на розв’язання.
5-6	Розв’язання в цілому вірне. Однак воно містить ряд помилок, або не                        розглянуті окремі випадки, але може стати правильним після невеликих                         виправлень або доповнень.
4	Правильно  розглянуто один з двох (більш складний) істотних випадків,                      або в задачі типу «оцінка-приклад» вірно отримана оцінка.
2-3	Доведені допоміжні твердження, що допомагають у розв’язанні задачі.
0-1	Розглянуто окремі важливі випадки за відсутності розв’язання (або при                       помилковому розв’язанні).
0	Розв’язання неправильне, просування відсутні. Розв’язання відсутнє.

 Не можна зменшувати кількість балів за те, що розв’язання занадто довге. Виправлення в роботі (закреслення раніше написаного тексту) також не є підставою для зняття балів. У той же час будь-як завгодно довгий текст розв’язання, що не містить корисних просувань, повинен бути оцінений в 0 балів.