8 клас. ІІ етап математичної олімпіади.

Другий етап Всеукраїнської олімпіади юних математиків 2012 р.

Завдання

                                       8 клас

1.  На сторонах АВ, ВС,АС правильного трикутника АВС зі стороною З см позначили точки L, К, М відповідно, так, що LВ = КС = АМ = 1см. Доведіть, що трикутник КLМ правильний.
2. При яких цілих  m значення виразу 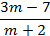    буде натуральним  числом?
3. 20 % родин міста X, які мають кішок (хоча б одну кішку), також мають і собак (хоча б одного собаку). 25% родин цього міста, що мають собак, також мають і кішок. 20% не мають ані кішок, ані собак. Знайти відсоток мешканців міста, що мають, як кішок, так і собак. Відповідь обґрунтуйте.
4. Доведіть, що кількість 2013-цифрових чисел, складених з цифр 1, 2, З, 5 — парна
5. Усі точки площини пофарбовано в 4 кольори, причому кожен колір використовується. Чи обов’язково знайдеться пряма, що містить точки принаймні трьох різних кольорів?

На виконання завдань відводиться 4 години

Другий етап Всеукраїнської олімпіади юних математиків 2009 р.

Завдання

8 клас

1. При яких значеннях m рівняння

mx – 2008 = m -2008x  і  2009x = m – 2008x

мають спільний корінь?

2. Модуль значення виразу 3x + 1  не перевищує 5. Скільки різних цілих значень може набувати значення виразу 8x + 7?

3. Є 100 карток, у кожної із яких одна сторона чорна, а друга – біла. Усі ці картки лежать на столі білою стороною догори. Петрик спочатку перевертає 50 карток, потім якісь 60 карток, а потім ще якісь 70 карток. В кінцевому результаті усі 100 карток виявилися перевернутими чорною стороною догори. Скільки карток були перевернутими три рази? Вкажіть усі можливі відповіді і доведіть, що інших немає.

4. Іванко і Марічка живуть у висотному будинку, на кожному поверсі якого по 10 квартир. Номер поверху Іванка дорівнює номеру квартири Марічки, а сума номерів їх квартир дорівнює 239. Який номер квартири, в якій живе Іванко? Відповідь обґрунтуйте.

5.  У довільному  5-кутнику ABCDE  проведено усі діагоналі. В утвореній діагоналями п’ятикутній зірці ABCDE відомо, що кут АСЕ = куту ADB і кут DBЕ = куту BEC. Відомо також, що BD=CE. Доведіть, що кут АСD = куту ADC.


Другий етап Всеукраїнської олімпіади юних математиків 2010 р.
                                     8 клас

1.У краплю води, де знаходилися 1000 бактерій, посадили один вірус. Після цього кожну хвилину стало відбуватися наступне: кожен вірус знищував по одній бактерії, після чого кожна бактерія ділилася на дві бактерії, а кожен вірус – на два віруси. Чи вірно, що через деякий час не залишиться жодної бактерії?

2. Кожний з чотирьох гномів – Беня, Веня, Євген, Сеня – або завжди говорить правду, або завжди бреше. Ми почули таку розмову. Веня – Бені: «Ти брехун». Євгену – Веню: «Сам ти брехун». Сеня – Євгену: «Та обидва вони брехуни, (подумавши) втім, і ти теж». Хто з них говорить правду?

3. Усередині опуклого 10-кутника відзначили 10 точок і розбили його на трикутники з вершинами в цих  точках і вершинах 10-угольника. Чи може при цьому вийти 30 трикутників?

4. По кругу стоять числа 1, 2. 3, 4, 5, 6, 7, 8. Дозволяється узяти будь-які два сусідні числа і замість них записати на їх місця середнє арифметичне цих чисел. Чи можна, повторивши багато раз цю операцію, отримати 8 однакових чисел?

5. Послідовні непарні числа згруповані таким чином: (1)  (3,5)  (7,9,11) (13,15,17,19) ... Знайдіть суму чисел в сотій групі.

На виконання роботи виділяється 4 години.

Використання записників і калькулятора не дозволяється.

Кожна задача оцінюється в 7 балів 

Загальні критерії оцінювання завдань наведено в таблиці.

7	Повне правильне розв’язання
6-7	Повне правильне розв’язання. Є невеликі недоліки, які в цілому не впливають на розв’язання.
5-6	Розв’язання в цілому вірне. Однак воно містить ряд помилок, або не                        розглянуті окремі випадки, але може стати правильним після невеликих                         виправлень або доповнень.
4	Правильно  розглянуто один з двох (більш складний) істотних випадків,                      або в задачі типу «оцінка-приклад» вірно отримана оцінка.
2-3	Доведені допоміжні твердження, що допомагають у розв’язанні задачі.
0-1	Розглянуто окремі важливі випадки за відсутності розв’язання (або при                       помилковому розв’язанні).
0	Розв’язання неправильне, просування відсутні. Розв’язання відсутнє.

 Не можна зменшувати кількість балів за те, що розв’язання занадто довге. Виправлення в роботі (закреслення раніше написаного тексту) також не є підставою для зняття балів. У той же час будь-як завгодно довгий текст розв’язання, що не містить корисних просувань, повинен бути оцінений в 0 балів.