Середнє арифметико-геометричне — це спільна границя двох послідовностей, середньої арифметичної та середньої геометричної двох заданих чисел a та b.
Доведення[ред. • ред. код]
Нехай нам задано два додатніх числа a та b, причому (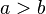 ). Складемо їх середнє арифметичне та середнє геометричне.
). Складемо їх середнє арифметичне та середнє геометричне.
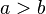 ). Складемо їх середнє арифметичне та середнє геометричне.
). Складемо їх середнє арифметичне та середнє геометричне.
Відомо, що перше середнє більше за друге:
В той же час, вони містяться між заданими числами:
Якщо числа  та
та 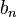 вже визначені, то
вже визначені, то  та
та 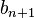 визначаються за формулами:
визначаються за формулами:
 та
та 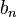 вже визначені, то
вже визначені, то  та
та 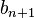 визначаються за формулами:
визначаються за формулами:
і, як і вище, 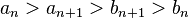
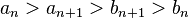
Таким чином складаються дві варіанти  та
та 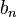 , перша з яких є спадною, а інша зростаючою (на зустріч одна одній). В той же час
, перша з яких є спадною, а інша зростаючою (на зустріч одна одній). В той же час
 та
та 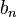 , перша з яких є спадною, а інша зростаючою (на зустріч одна одній). В той же час
, перша з яких є спадною, а інша зростаючою (на зустріч одна одній). В той же час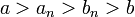
Так що обидві варіанти обмежені, і відповідно, обидві прямують до кінцевих границь.

Якщо в рівнянні
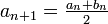
перейти до границь, то отримаємо

звідкіля
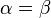
Таким чином, обидві послідовності прямують до спільної границі 

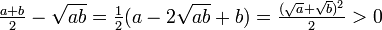

Немає коментарів:
Дописати коментар