Чітка логіка
Філософія математики — розділ філософії (філософія предметної області), що досліджує філософські припущення, основи і наслідки математики. Метою філософії математики є оцінка природи і методології математики і розуміння місця математики в житті людей. Філософія математики є розділом філософії науки і близька до метаматематики. Логічна та структурна природа самої математики робить філософські дослідження математики одночасно широкими і унікальними серед інших розділів філософії.
Основоположне питання філософії математики полягає у встановленні взаємовідносин між математичними поняттями і теоріями з одного боку, та реальним світом — з іншого.
Головні теми (питання), які розглядає філософія математики:
- Що є джерелами математичного змісту?
- Що таке онтологічний статус математичних сутностей?
- Що відносимо до математичних об'єктів?
- Яка особливість математичного судження ?
- Який зв'язок між логікою і математикою?
- Яка роль герменевтики в математиці?
- Які дослідження відіграють важливу роль в математиці?
- Які цілі математичного дослідження?
- Що отримує математика від спирання на досвід?
- Які людські особливості лежать в основі математики (гуманістичний аспект математики)?
- Що таке краса математики (естетика математики)?
- Що є джерелом і яка природа математичної істини?
- Який зв'язок між абстрактним світом математики і матеріальним всесвітом?
Існують філософія математики і математична філософія, які деколи вживаються як синоніми, однак вони охоплюють різні царини досліджень і є окремими розділами філософії. Дослідження математичної філософії стосуються проекту формалізації філософських галузей, скажімо, естетики, етики, логіки,метафізики, або богослов'я, в нібито точніші і строгіші форми, як, наприклад, праці схоластичних богословів або прагнення систематизації Лейбніца і Спінози. Також математичну філософію пов'язують з практичною філософією окремих математиків чи співтовариств математиків-однодумців. Крім того, дехто розуміє термін "математична філософія", як натяк на підхід Бертрана Рассела до філософії і математики, який він виклав у своїх книгах "Принципи математики" і "Вступ у математичну філософію".
Металогіка — вивчення метатеорії логіки. На відміну від логіки, яка досліджує способи застосування логічних систем для доведень і спростувань, металогіка досліджує властивості самих логічних систем. Виділяють синтаксис логічний і семантику в логіці.
Область дослідження металогіки: формальні мови, формальні системи та їх інтерпретації.
Окремі питання металогіки відомі з часів Аристотеля, однак тільки з появою формальних мов у кінці XIX ст — на поч. XX ст. цей напрямок у науці отримав свій розвиток.
Металогіка і метаматематика часто розглядаються як синоніми та вивчаються в рамах математичної логіки.
Математи́чна ло́гіка є
наукою про закони математичного мислення.
Предметом математичної логіки є математичні теорії в цілому, які вивчаються за
допомогою логіко-математичних мов. При цьому в першу чергу цікавляться
питаннями несуперечливості математичних теорій, їх розв'язності та повноти.
Математична логіка по суті є формальною логікою, що використовує
математичні методи. Формальна логіка вивчає акти мислення (поняття, судження,
умовиводи, доведення) з точки зору їх форми, логічної структури, абстрагуючись
від конкретного змісту. Творцем формальної логіки є Арістотель, а першу завершену систему математичної логіки на
базі строгої логіко-математичної мови — алгебру логіки, —
запропонував Джордж Буль (1815—1864). Логіко-математичні
мови і теорія їх смислу розвинуті в роботах Готлоб Фреге(1848—1925), який ввів поняття
предикату і кванторів. Це надало можливість застосувати логіко-математичні мови
до питань основ математики. Виклад цілих розділів математики на мові
математичної логіки та аксіоматизація арифметики зроблені Джузеппе Пеано (1858—1932). Грандіозна спроба
Г.Фреге та Бертран Рассел (1872—1970) зведення всієї
математики до логіки не досягла основної мети, але привела до створення
багатого логічного апарату, без якого оформлення математичної логіки як повноцінного
розділу математики було б неможливе.
На межі 19 століття-20 ст. були відкриті парадокси, зв'язані з основними
поняттями теорії множин(найвідомішими є парадокси Георг Кантор та Б. Рассела). Для виходу з
кризи Л. Брауер (1881—1966) висунув
інтуїціоністську програму, в якій запропонував відмовитися від актуальної
нескінченності та логічного закону виключеного третього, вважаючи допустимими в
математиці тільки конструктивні доведення. Інший шлях запропонував Давид Гільберт (1862—1943), який в 20-х роках 20
ст. виступив з програмою обґрунтування математики на базі
математичної логіки. Програма Гільберта передбачала побудову формально-аксіоматичних
моделей (формальних систем) основних розділів математики та
подальше доведення їх несуперечливості надійними фінітними засобами.
Несуперечливість означає неможливість одночасного виведення деякого твердження
та його заперечення. Таким чином, математична теорія, несуперечливість якої
хочемо довести, стає предметом вивчення певної математичної науки, яку Давид Гільберт назвав метаматематикою, або
теорією доведень. Саме з розробки Д. Гільбертом та його учнями теорії доведень
на базі розвинутої в працях Готлоба Фреге та Бертрана Рассела логічної мови починається
становлення математичної логіки як самостійної математичної дисципліни.
Сфера
застосування математичної логіки дуже широка. З кожним роком зростає глибоке
проникнення ідей та методів математичної логіки в інформатику, обчислювальну математику, лінгвістику, філософію.
Потужним імпульсом для розвитку та розширення сфери застосування математичної
логіки стала поява електронно-обчислювальних
машин. Виявилося, що в рамках математичної логіки
вже є готовий апарат для проектування обчислювальної техніки. Методи і поняття
математичної логіки є основою, ядром інтелектуальних інформаційних систем.
Засоби математичної логіки стали ефективним робочим інструментом для фахівців
багатьох галузей науки і техніки.
В процесі розвитку, у логіку було впроваджено ряд розмежувань що допомагають формалізуванню різних форм логіки як науки. Приклади таких розмежувань наведено нижче.
Ло́гіка (грец. λογιχη від грец. logos — слово, сенс, думка,мова) — наука про закони і форми мислення, методи пізнання та умови істинності знань і суджень[1]. Головним об'єктом дослідження логіки є описові системи мислення, тобто системи, які пропонуються як інструкція для людей (а також, можливо інших розумних істот/машин) як слід правильно мислити. При цьому, такі інструкції не слід розглядати як опис того, як люди насправді мислять, що є предметом дослідження інших дисциплін, наприклад коґнітивної психології.
У щоденній мові, логіка є способом судження, що полягає в отриманні висновку із набору припущень. Формальніше, логіка стосується виведення — процесу що продукує нові твердження із вже встановлених. Саме тому у логіці особлива увага приділяється структурам виводу — конкретніше, формальним відношенням між вихідними твердженнями та висновками, де «формальний» означає що ці відносини є незалежними від самих тверджень. Не менш важливим є дослідженняістинності виводу, включаючи різноманітні можливі визначення істинності та передумови що на практиці уможливлюють її встановлення. Таким чином очевидною є важлива роль що її відіграє логіка у епістемології, забезпечуючи останню механізмом розширення знання.
Побічним продуктом логіки є рецепти мислення, тобто опис того як люди та інші розумні істоти/машини/системи повинні мислити. При цьому такі рецепти не є суттєвими для предмету самої логіки, але є радше одним із її практичних застосувань. Більш того, вони не повинні розглядатись як опис того як люди насправді мислять, що є предметом дослідження інших дисциплін, зокрема коґнітивної психології.
Традиційно логіка вивчається як галузь філософії. Починаючи із середини вісімсотих років минулого тисячоліття логіка стає предметом дослідження математики, а останнім часом і інформатики. Як наука, логіка досліджує та класифікує структури тверджень та аргументів та розробляє схеми їх кодифікації. Таким чином, предмет дослідження логіки може бути дуже широким, включаючи судження про ймовірність тапричинність. Логікою також досліджуються структури логічних хиб та парадокси. Стародавні греки поділялидіалектику на логіку та риторику. Риторика має справу з переконувальною аргументацією, що може певною мірою розглядатись як протиставлення логіці.
Історія логіки різних історичних періодів
Історія логіки
Історія логіки налічує приблизно 2,5 тис. років. Розрізняють два етапи логіки:
- традиційний етап. (IV ст. до н.е.- друга пол. XIX ст.)
- сучасний етап. (друга пол. XIX - до наших днів)
Традиційна та сучасна логіка суттєво відрізняються одна від одної. Але вони не заперечують одна одну. Одна є продовженням іншої.
Вперше логіка з'являється як наука в часи античності (IV - III ст. до н.е). А сам термін використовувся як філософський, і був введений Гераклітом приблизно 544-483рр. до н.е.). Логос позначався як вічна і всезагальна необхідність, певна стійка закономірність.
Традиційна логіка мала дві великі епохи свого піднесення - античність та середьовіччя. Після цих епох логіка практично не розвивалась, хоча користувалась певною повагою за минулі досягнення. Її вивчення було обов'язковим у середні віки як один із складників тривіуму - логіка, риторика, граматика. А надалі логіка була одним іх основних предметів у всіх західно-європейських університетах. Вважалось, що логіка мерта наука, яка вже дала все, що могла. Іммануїл Кант стверджував, що логіка була завершеною наукою від самого початку і вона не зробила жодного кроку вперед від часів Аристотеля.
Традиційна логіка
Античність
В цей період логіка розвивалась не надто активно. Цей період характеризується спадами та різкими зацікавленнями до логіки. Засновкником традиційної логіки вважають Аристотеля (Стагиріта). Часто традиційну логіку називають аристотелівською логікою. Саме за його часу логіка досягла найвищого розквіту. Його заслуга полягає в тому, що він узагальнив та систематизував дослідження з логіки його попередників (мілетська школа, софісти, Демокрит, Сократ та ін.), попередні дослідження були вкрай несистематичним і сприймались лише в контексті філософії, риторики, граматики, створив першу теорію висновку (силогізм), визначив головні форми та закони мислення. Аристотель присвятив значну кількість своїх філософських творів працям з логіки. А Андронік Родоський, послідовник Стагиріта, об'єднав їх в трактаті "Органон", назву якого можна перекласти як знаряддя, засіб, інстумент.
Стоїки
Значний внесок у розвиток логіки зробила мегаро-стоїчна школа. Її представники : Зенон, Хризіпп, Діодор, Стільпон, Евбулід, Філон. Хрисіпп фактично розробив стоїчну концепцію логіки
Стоїки вивчали логічні відношення між висловлюваннями і цим заклали підвалини одного з розділів сучасної логіки - логіки висловлювань. Стоїки сформулювали визначення матеріальної імплікації, кон'юнкції, диз'юнкції, еквіваленції, заперечення.
Логіка середньовіччя
Епоха Середньовіччя це друга епоха звеличення логіки. Вона тривала з серед. XII ст. до серед. XIV ст. Одним з головних вчень логіки середньовіччя є вчення про суппозиції.
Петро Іспанський значна постать в історії логіки. Його праця "Суммули", був основним підручником з логіки в середньовіччі. Михайло Псьол - відомий логік, візантійський письменник, філософ, державний діяч. Він ввів у логіку схемі під назвою "логічний квадрат", дав назви модусам простого категоричного міркування й дав позначення для категоричного судження.
І хоч логіку поважали, вона була у стані сплячки - її використовували для структуруванні церковних догматів та дискусіях на релігійну тему. Панівною була схоластична логіка.
Відродження й Новий час[
Цей період важливий насамперед великою кількістю нових публікацій. В 1662 р.в Парижі П. Ніколь та А. Арно видають підручник "Логіка Пор-Рояля", 1620р. Френсіс Бекон пише "Новий Органон".
Френсіс Бекон був першим, хто виступив проти схоластичної логіки, стверджуючи, що логіка мусить бути живою наукою, давати нові відкриття. Тому, бажаючи показати своє новаторство і відмінність від Аристотеля, логіка якого цього не здійснила, він показово називає свою працю "Новий Органон". Бекон проголосив боротьбу проти "ідолів" або "привидів" - це тріднощі які виникають у процесі пізнання. Він виділив 4 найхарактерніших ідолів:
- "ідоли роду" - створені в результаті намагання наділити явища природи людськими якостями. Людина часто тлумачить неживий світ за аналогією з собою(сумне небо, ласкаве сонце і т.п.) Цей ідол є наймогутнішим, адже він вплетений в життя кожної людини.
- "ідоли печери" - помилкові відображення дійсності, які виникають внаслідок надмірної схильності людини до старих істин, або нових відкриттів.
- "ідоли ринку" - труднощі пізнання, які виникають в результаті некритичного, поверхневого ставлення до функцій, значення, природи слова.
- "ідоли театру" - хибні твердження, що обґрунтовуються посиланнями на авторитет.
Справжнім методом пізнання, за Беконом, є індукція.
Сучасна логіка
Сучасна логіка сформувалась наприкінці XIX - на початку XX ст. Її засновником вважається ГотфрідЛяйбніц, який жив в XVII ст. Але його ідеї значно випереджали його час і не були сприйняті сучасниками. І лише у XX ст. з розвитком логічних знань його ідеї почали розвиватись у працях інших науковців.
На цьому етапі розвитку логічного знання інтереси логіків значно розширюються. Вони починають звертатись до таких типів міркувань , яким раніше було відмовлено в можливості логічного аналізу. Починається дослідження практичних міркуваннь, які мусять пояснити дії людини.
Сучасна логіка поділяється на класичну та некласичну логіку.
Класична логіка
Класична логіка повністю орієнтується на аналіз математичних міркувань. Вона призначена для того, аби розв'язати проблему основ математичного знання. Було здійснено перенесення в логіку методів, які застосовуються в математиці. Відбулося створення таких розділів логіки, як логіка висловлювань та логіка предикатів.
Представники: Джордж Буль, Огастес де Морган, Чарльз Пірс, Готліб Фреге, Давід Гільберт та ін.
Першою великою працею є "Принципи математики" Б.Рассела та А. Уайтхеда
Некласична логіка
Некласична логіка виникає з критики класичної логіки. Важко дати визначення некласичній логіці так як вона розглядає різні типи міркувань. Мета некласичної логіки полягає в описані тих видів міркувань, які не розглядаються класичною логікою. Їснує дуже багато розділів некласичної логіки і їх кількість збільшується. Деякі розділи некласичної логіки:
- алетична логіка
- логіка часу (темпоральна логіка)
- епістемічна логіка
- логіка норм (деонтична логіка)
- логіка оцінок (аксіологічна логіка)
- логіка дії
та ін.
Логіка Індії
Розвиток логіки в Індії поділяють на три періоди:
- рання будистська логіка (VI-V ст. до н.е.- II ст. н.е)
- діяльність логічних шкіл ньяя і вайшешика (III ст. н.е.- V ст. н.е.)
- розквіт будистської логіки (VI ст. н.е. - VIII ст. н.е.)
Індійська логіка виникла незалежно та відрізняється від логіки Давньої Греції наявністю в силогізмі не 10, а 5 членів, дедукція та індукція є одним цілим, відрізняють мову мисленнєву та словесну, судження є частиною висновку, основою сприйняття є набутий досвід.
Філософська школа ньяя займалась методологією пізнання. В цій даршані вважалось, що шляхом звільнення від стираждань є досягнення абсолютного знання, а логіка дозволяє повніше поглянути і зрозуміти світ та себе, дозволяє отримати правдиву інформацію. Ньяя не використовувала символи, а замінювала їх складними кліше. Деякі дослідники вважають, що пізня ньяя перевершила вчення Аристотеля.
Буддійська філософія була опонентом ньяї. Фундатором буддистської логіки був Дігнаг, автор " Про джерела пізнання". Він ввів логіку у ранг науки.
Логіка Китаю
Логіка в Стародавньому Китаї зародилась в Золотий вік китайської філософії. Цей час відрізнявся великою кількістю філософських шкіл ("суперництво ста шкіл") та появою філософських дискусій. На розвиток логіки вплинули діяльність шкіл номіналістів (мінцзя, або школа імен), легістів (фацзя, або школа закону), конфуціанство (жуцзя) та моїзм (моцзя). Але тільки остання об'єднала несистематичні та розкидані по різним школам знання в одному акті. Саме моїсти створили перший в Китаї трактат з логіки - "Мобянь".
Фундатором китайської логіки вважається Мо-цзи, який був суперником Конфуція, що теж розвивав ідеї логіки. Його філософська школа моїзму займалась витоками правильного висновку та правилами його отримання. Основним методом аргументації було міркування за аналогією. Моїсти багато уваги приділяли семантиці. Вони розробили методи класифікації імен за ступенем їх загальності, аналізуючи семантику мови. Були створені два методи моїзму: "метод трьох правил" та "метод трьох фа".
Логіка Китаю хоч і виникла раніше за логіку Давьої Греції, все ж не розвинулась, не структурувалась та залишилась в зародковому стані, через використання логіки виключно в прикладних цілях.
Дедукція та Індукція
Оригінально, логіка складалась лише із дедукції, що досліджує універсальні правила виводу із заданих тверджень. Однак важливо зауважити, що часом включають в курс логіки також індукцію — науку про виведення достовірних узагальнень із спостережень. Відповідно важливим є розрізнення дедуктивної істинності та індуктивної істинності. Виведення є дедуктивно істинним тоді і лише тоді, якщо неможлива ситуація коли всі припущення істині а вивід ні. Поняття дедуктивної істинності може бути строго сформульоване для систем формальної логіки побудованих із використанням ґрунтовно дослідженої термінології семантики. З іншого боку, індуктивна істинність вимагає спершу дати визначення достовірному узагальненню деякої множини спостережень. Існують різні підходи до цієї задачі, більш або менш формальні; деякі з них використовують математичні ймовірнісні моделі. Надалі мова йтиме головним чином про дедуктивну логіку.
ДВІЙКОВА ЛОГІКА
Алгебра
логіки (Булева логіка, двійкова
логіка, двійкова алгебра) —
розділ математичної логіки, що вивчає систему логічних операцій над висловлюваннями. Тобто, представлення логіки у вигляді алгебраїчної структури.
Визначення
Базовими елементами, якими оперує алгебра логіки, є висловлювання. Висловлювання будуються над множиною {B,  ,
,  ,
,  , 0, 1}, де B - непорожня множина, над елементами якої визначені три операції:
, 0, 1}, де B - непорожня множина, над елементами якої визначені три операції:
 ,
,  ,
,  , 0, 1}, де B - непорожня множина, над елементами якої визначені три операції:
, 0, 1}, де B - непорожня множина, над елементами якої визначені три операції:
а також константи - логічний нуль 0 і логічна одиниця 1.
Аксіоми[ред. • ред. код]
Походження[ред. • ред. код]
Засади алгебри логіки були сформульовані британцем Джорджем Булем в 1847 році. Пізніше її розвивалиЧарлз Пірс, Генрі Шеффер, П. С. Порецький, Бертран Рассел, Давид Гільберт та ін.
Відтоді ця система застосовується для вирішення широкого спектру проблем математичної логіки та теорії множин, та особливо конструювання цифрової електроніки (початок використання алгебри логіки для синтезу перемикальних (релейних) схем був покладений в 1938 році роботами відомого американського вченого Клода Шеннона).
Предмет вивчення[ред. • ред. код]
Спочатку проблематика алгебри логіки перетиналась з проблематикою алгебри множин (теоретико-множинні операції).
Проте з закінченням формування теорії множин (70-і роки 19 ст.), яка включила в себе алгебру множин, і подальшим розвитком математичної логіки, предмет алгебри логіки значно змінився.
Сучасна алгебра логіки розглядає операції над висловлюваннями (див. Числення висловлень), як булеву функцію і вивчає відносно них такі питання, як:
- таблиці істинності;
- функціональна повнота;
- замкнені класи;
- представлення у вигляді: ДНФ, КНФ, полінома Жегалкіна.
Логічні операції[ред. • ред. код]
Простим і найширше вживаним прикладом такої алгебраїчної системи є множина B, що складається всього з двох елементів :
- B = { Хибність(0), Істина(1) }
Як правило, в математичних виразах Хибність ототожнюється з логічним нулем, а Істина - з логічною одиницею, а операції заперечення(НІ), кон'юнкції(ТА) і диз'юнкції(АБО) визначаються в звичному нам розумінні. Легко показати, що на цій множині B можна задати чотири унарні і шістнадцять бінарних відношень і усі вони можуть бути отримані через суперпозицію трьох обраних операцій.
Спираючись на цей математичний інструментарій, логіка висловлювань вивчає висловлювання і предикати. Також вводяться додаткові операції, такі як еквівалентність  ("тоді і тільки тоді, коли"), імплікація
("тоді і тільки тоді, коли"), імплікація  ("отже"), складання по модулю два
("отже"), складання по модулю два  ("що виключає або»), штрих Шеффера
("що виключає або»), штрих Шеффера  , стрілка Пірсу
, стрілка Пірсу  та інші.
та інші.
 ("тоді і тільки тоді, коли"), імплікація
("тоді і тільки тоді, коли"), імплікація  ("отже"), складання по модулю два
("отже"), складання по модулю два  ("що виключає або»), штрих Шеффера
("що виключає або»), штрих Шеффера  , стрілка Пірсу
, стрілка Пірсу  та інші.
та інші.
Логіка висловлювань послужила основним математичним інструментом при створенні комп'ютерів. Вона легко перетворюється в бітову логіку: істинність висловлювання позначається одним бітом (0 - ХИБНІСТЬ, 1 - ІСТИНА); тоді операція  набуває суті вирахування з одиниці;
набуває суті вирахування з одиниці;  - немодульного складання; & - множення;
- немодульного складання; & - множення;  - рівності;
- рівності;  - в буквальному розумінні сума за модулем 2(що виключає АБО - XOR);
- в буквальному розумінні сума за модулем 2(що виключає АБО - XOR);  - сума не перевищує 1 (тобто A
- сума не перевищує 1 (тобто A  B = (A + B) <= 1).
B = (A + B) <= 1).
 набуває суті вирахування з одиниці;
набуває суті вирахування з одиниці;  - немодульного складання; & - множення;
- немодульного складання; & - множення;  - рівності;
- рівності;  - в буквальному розумінні сума за модулем 2(що виключає АБО - XOR);
- в буквальному розумінні сума за модулем 2(що виключає АБО - XOR);  - сума не перевищує 1 (тобто A
- сума не перевищує 1 (тобто A  B = (A + B) <= 1).
B = (A + B) <= 1).
Згодом булева алгебра була узагальнена від логіки висловлювань шляхом введення характерних для логіки висловлювань аксіом. Це дозволило розглядати, наприклад, логіку кубітів, потрійну логіку(коли є три варіанти істинності висловлювання : "істина", "хибність" і "невизначено") та ін.
Властивості логічних операцій[ред. • ред. код]
- Комутативність: x
 y = y
y = y x,
x,  {&,
{&, 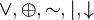 }.
}. - Ідемпотентність: x
 x = x,
x = x,  {&,
{&,  }.
}. - Асоціативність: (x
 y)
y) z = x
z = x (y
(y z),
z),  {&,
{&,  }.
}. - Дистрибутивність кон'юнкцій і диз'юнкції відносно диз'юнкції, кон'юнкції і суми за модулем два відповідно:
 ,
,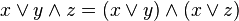 ,
, .
.
- Законы де Мо́ргана:
 ,
, .
.
- Закони поглинання :
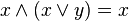 ,
, .
.
- Інші (1):
- Інші(2) :
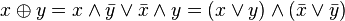 .
.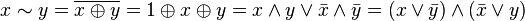 .
. .
. .
.
- Інші(3) (Доповнення законів де Мо́ргана) :
 .
. .
.
Існують методи спрощення логічної функції : наприклад, Карта Карно, метод Куайна - Мак-Класкі
Багатозначна логіка — тип формальної логіки,
характерний наявністю більш ніж двох можливих істинних значень (істинності та хибності).
Першу систему багатозначної
логіки запропонував польський математик Ян Лукасевич в
1920 році. В наш час існує
дуже багато інших систем багатозначної логіки, які в свою чергу можуть бути
згруповані за класами. Найважливішими з таких класів є часткові
логіки та нечіткі логіки.
Форма́льна
ло́гіка — конструювання і дослідження правил
перетворення висловів, що зберігають своє істинне значення безвідносно до
змісту вхідних в ці вислови понять. У історії філософії —
окремий розділ або напрям логіки кінця XIX — початку XX ст. У сучасному
вжитку — синонім символічної,
або математичної логіки.
Тризначні логіки
тризначна логіка була
історично першою багатозначною логікою, і є найпростішим розширенням двозначної
логіки. Перелік істиннісних значень тризначної логіки крім «істинно» та «хибно»
включає також третє значення, яке як правило трактується як «невизначене»,
«невідомо» або «помилково». В останньому випадку логіку зазвичай
називають частковою.
У тризначній логіці природно не
дотримується закон
виключеного третього. Разом з тим, важливою властивістю тризначних
логік, що відображає їх адекватність, є те,
що всі вони являють собою розширеннякласичної двозначної
логіки. Тобто, за припущення, що символи, які інтерпретуються, не
приймають третього істиннісного значення, семантик а формул в
тризначній логіці така ж, як і в двозначній.
Скінченнозначні логіки
Скінченнозначні логіки (інша
назва — 'k'-значні) є узагальненням двозначної логіки в
тому, що функція в ній може приймати не два значення (0 і 1), а значення від 0
до k-1. Істотною відмінністю 'k'-значної логіки від двозначної є той факт, що
наразі не існує повного опису замкнених класів при k>2. У двозначній логіці
навпаки існує повний опис системи
замкнутих класів, запропонований Емілем Постом у 1940 році.
Існують наступні перепозначення для
функцій кон'юнкції та диз'юнкції:
·
A ∧ B = min (A, B)
·
A ∨ B = max (A, B)
Нескінченнозначні логіки
Нескінченнозначну логіку можна ввести
наступним чином:
·
Істинне значення знаходиться на відрізку дійсних чисел від 0 до 1;
·
Заперечення визначається як: ¬ A = 1-A;
·
Кон'юнкція визначається як: A ∧ B = min (A, B);
·
Диз'юнкція визначається як: A ∨ B = max (A, B).
До формальних систем нескінченнозначної
логіки можуть бути віднесені системи R-функцій В. Л. Рвачова[1].
Теорія ймовірностей і багатозначні логіки
Може здатися, що теорія ймовірностей дуже
схожа на нескінченнозначну логіку: ймовірності відповідає істинне значення (1 =
істина, 0 = брехня), ймовірність ненастання якої-небудь події відповідає
запереченню, ймовірність одночасного настання двох подій відповідає кон'юнкції,
а ймовірність настання хоча б одніє з двох подій відповідає диз'юнкції.
Однак між багатозначними логіками і
теорією ймовірностей є принципова відмінність: в логіках істинне значення
будь-якої функції цілком визначається істинними значенням її аргументів, тоді
як в теорії ймовірностей, ймовірність складеної події залежить не тільки від
ймовірностей подій-компонентів, але і від їх залежності один від одного (що
виражається через їх умовні ймовірності).
Це проявляється, зокрема, в тому, що в
теорії ймовірностей виконується еквівалент «закону виключеного третього»:
ймовірність того, що деяка подія {відбудеться чи не відбудеться}, завжди
дорівнює одиниці, тоді як у багатозначних логіках закон виключеного третього не
виконується.
У теорії ймовірностей виконується також
еквівалент «закону протиріччя»:
ймовірність того, що {деяка подія одночасно настане і не настане}, завжди
дорівнює 0, тоді як в багатозначних логіках закон протиріччя не виконується.
Також існує певний зв'язок між істинними
значеннями нескінченновимірної логіки та ймовірностями теорії ймовірностей, а
саме:
·
Якщо a- ймовірність деякої події, то ймовірність ненастання
цієї події становить 1-a;
·
Якщо a і b- ймовірності деяких двох подій, то
ймовірність спільного настання цих двох подій не перевищує min(a,b);
·
Якщо a і b- ймовірності деяких двох подій, то
ймовірність настання хоча б однієї з цих двох подій більша, або дорівнює max(a,b).
Нечітка логіка
Нечітка, або ж «розмита», логіка (від англ. fuzzy logic) як наука була
започаткована американським вченим іранського походження Лотфі А. Заде (Lotfi A. Zadeh). На відміну від булевої алгебри,
у котрій існує лише дві величини (0 та 1, правда чи неправда) у нечіткій логіці
існують також перехідні величини (стани).
Одні з основних понять нечіткої
логіки: нечіткі множини, фазіфікація/дефазіфікація, фазі-операція.
В останні роки значення
нечіткої логіки стрімко виросло у світі високих технологій.
Математичні
основи
Символічна нечітка логіка Символічна нечітка логіка засновується на
понятті t-норми. Після вибору деякої t-норми з'являється можливість визначити
основні операції: кон'юнкцію диз'юнкцію, імплікацію, заперечення та ін.
Неважко довести теорему про те,
що дистрибутивніть, притаманна класичній логіці, виконується тільки у випадку
якщо t-норма є t-нормою Геделя.
Нечітка логіка та нейронні
мережі Оскільки
нечіткі множини описуються функціями належності, а t-норми та k-норми
звичайними математичними операціями, можна уявити нечіткі логічні міркування у
вигляді нейронної мережі. Для цього функції приналежності треба інтерпретувати
як функції активації нейронів, передачу сигналів як зв'язку, а логічні t-норми
та k-норми, як спеціальні види нейронів, що виконують математичні відповідні
операції. Існує велика різноманітність подібних нейро-нечітких мереж.
Наприклад, ANFIS (Adaptive Neuro fuzzy Inference System) - адаптивна
нейро-нечітка система виводу.
Вона може бути описана в універсальній формі апроксиматорів як
 ,
,
крім, того цією формулою можуть біти описані деякі нейронні мережі, так як радіально базисні мережі (RBF),багатошарові персептрони (MLP), а також вейвлети і сплайни.
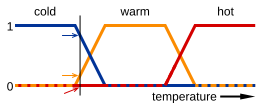
Приклад визначення лінгвістичної змінної[ред. • ред. код]
У визначеннях, принятих для лінгвістичної змінної:
- X = «Температура в кімнаті»
- U = [5, 35]
- T = {«холодно», «комфортно», «жарко»}
Характеристичні функції:
Правило G породує нові терми з використанням звязок «і», «або», «не», «дуже», «біль менш».
- не A:

- дуже A:
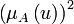
- більш меньш A:

- A або B:

- A і B:
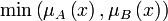

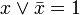

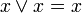
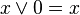

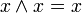
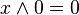
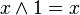
 .
. .
. .
.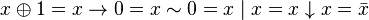 .
.
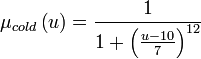
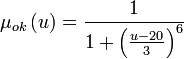

Немає коментарів:
Дописати коментар